Методика формализации междисциплинарных факторов и критериев оптимизации региональных систем экономики
Technique of formalization of interdisciplinary factors and criteria for the optimization of regional economic systems
Авторы
Аннотация
Статья продолжает исследование транспортной системы региона, служащей каркасом экономической системы. Предложена методика формализации междисциплинарных данных и знаний экономической географии, управления транспортом и пространственной экономики, применяемых в оптимизационной модели. Методика реализована системой поддержки принятия решений, основанной на методах теории ситуационного управления. Построены модели, дополняющие исходную методику, и являющиеся отдельным исследовательским инструментом с перспективой применения искусственного интеллекта.
Ключевые слова
Развитие региональной транспортной инфраструктуры, пространственно-локализованная экономическая система, многокритериальная оптимизация, формализация данных и знаний, семиотическая модель, фреймовое представление знаний
Финансирование
Исследование поддержано РФФИ, проект №16-36-00385
Рекомендуемая ссылка
Методика формализации междисциплинарных факторов и критериев оптимизации региональных систем экономики// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №2 (54). Номер статьи: 5405. Дата публикации: 18.04.2018. Режим доступа: https://eee-region.ru/article/5405/
Authors
Abstract
The article continues the study of the transport system of the region, which serves as the frame of the economic system. The methodology of formalization of interdisciplinary data and knowledge of economic geography, transport management and spatial economics used in the optimization model is proposed. The methodology is implemented by a decision support system based on methods of situational management theory. The models complementing the original methodology are constructed and are a separate research tool with the prospect of using artificial intelligence.
Keywords
Development of regional transport infrastructure, spatially localized economic system, multi-criteria optimization, formalization of data and knowledge, semiotic model, frame representation of knowledge.
Project finance
The study was supported by RFBR, project №16-36-00385
Suggested Citation
Technique of formalization of interdisciplinary factors and criteria for the optimization of regional economic systems// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №2 (54). Art. #5405. Date issued: 18.04.2018. Available at: https://eee-region.ru/article/5405/
Введение
Настоящая публикация является продолжением исследования [1], которое посвящено проблеме оптимизации транспортной инфраструктуры региона в контексте формирования инфраструктурного каркаса его экономического развития. Ранее разработана методика, реализующая междисциплинарный многокритериальный анализ транспортной сети, направленный на ее оптимизацию в контексте проектов экономического развития регионов. Такой подход направлен на формирование транспортной сети не только как таковой, но в первую очередь, как основу инфраструктурного каркаса, обеспечивающего социальные и экономические связи, способствуя интенсификации процессов развития.
Постановка задачи
Разработанная ранее методика междисциплинарного исследования базируется на применении модели транспортной сети региона, в основе которой лежит гиперграф. На предыдущем этапе исследования предложены алгоритмы оптимизации транспортной сети, в ходе которых критерии оптимальности формируется на 4-х уровнях иерархической модели. На первом (базовом) уровне вектор критериев оптимальности формируется с применением данных и знаний в области управления транспортом, на втором и третьем – различных отраслей экономической географии, на четвертом – пространственной экономики. Таким образом, структура модели и методы ее реализации позволяют формализовать зависимость экономического развития территории от наличия и качества транспортной сети, расположенной на ней.
В ходе проделанной в рамках исследования [1] работы были определены параметры, являющиеся факторами векторов критериев оптимизации. Эти параметры расположены на разных уровнях иерархической модели и при рассмотрении их в плоскости каждого уровня они могут быть проанализированы в рамках теорий отдельных научных отраслей. Однако, строго говоря, предложенные структура модели и вектор критериев оптимальности являются только частным случаем решения задачи. В общем случае постановки задачи для реализации преимуществ междисциплинарного характера исследования необходимо обеспечить возможность вариативности количества уровней (слоев) модели, а кроме того исследуемых факторов и критериев каждого уровня. В том числе необходимо найти методы и пути формализации информации междисциплинарных знаний о том, какое влияние оказывают параметры друг на друга и при том не только внутри слоя, но и с учетом межслоевых зависимостей. В конечном итоге, в результате исследователь должен получить возможность определять с помощью полученной математической модели явные критерии оптимизации, опираясь на известные положения научных теорий, а структура и технология модели должны накапливать информацию и, формализуя данные, помогать найти неявные критерии оптимизации. Такой подход призван повысить качество результатов междисциплинарных исследований, находящихся на стыке проблем региональных транспортных и экономических систем.
Современное состояние вопроса. Методы и алгоритмы решения задачи
Исследование больших систем всегда сопряжено с трудностями абстрагирования реального объекта и протекающих в нем процессов до модели и формализации собранных данных в информацию пригодную для описания системы. На практике, чем больше допущений и упрощений можно применить при построении модели, тем более строгой и детерминированной она будет. Традиционно декомпозиция системы и определение вектора критериев оптимальности по возможности – единственного, является основным инструментом системного анализа. Однако такой подход в первую очередь применяется для исследования технических систем, например, таких как, электродвигатель, автомобиль, космический корабль, атомная электростанция и др. Для таких исследуемых объектов критерии оптимальности очевидны, т.к. цели существования и функционирования этих систем четко заданы, а параметры системы в высокой степени поддаются управлению. Следствием сказанного ранее является то, что получают оптимизационные модели, которые после расчета дают четко определенную готовую к использованию информацию. Например, результатами моделирования указанных систем будут: мощность электродвигателя, потребление топлива автомобилем на 100 км пробега и т.п. Полученные с помощью таких моделей данные не требуют дальнейшей экспертной оценки, гарантированно получаются в результате разыгрывания модели и однозначно определены для объекта исследования в заданных заранее условиях. Тем не менее такой подход декомпозиции и упрощения систем не всегда удовлетворяет нашим потребностям знания об объекте, либо недостижим с помощью известных теорий и методов исследования. С развитием ЭВМ и систем искусственного интеллекта анализу подвергается все большее количество сложных систем различного рода. Как правило, такие системы описываются с помощью анализа множества данных в условиях наличия неопределенностей. Отмеченные обстоятельства требуют применения, например, робастных моделей систем, а также моделей, которые требуют участия эксперта или агента искусственного интеллекта. Более того, для таких систем зачастую невозможно говорить об оптимальности, а значит задача оптимизации в классической постановке здесь становиться неправомочной [2].
В рассматриваемом нами случае [1] мы имели дело с несколькими подсистемами, находящимися в иерархической зависимости. Во-первых, исследовалась система транспортной сети, расположенной на полигоне заданного региона, во-вторых, система самого полигона с его географическими свойствами, в-третьих, экономическая система региона на заданном полигоне. Применённый ранее метод декомпозиции иерархической системы выявил необходимость дополнительного анализа, о котором говорилось выше. В качестве его инструментов выбраны теория и методы исследования проблем ситуационного управления [2-6]. Ситуация системы есть оценка (анализ, обобщение) совокупности характеристик объектов и связей между ними, которые состоят из постоянных и причинно-следственных отношений, зависящих от произошедших событий и протекающих процессов [2, 6]. С помощью методов ситуационного управления, адаптированных к задачам настоящего исследования, строится система поддержки принятия решения (СППР). Для целей настоящего исследования принято определение СППР приводимое в [6]: «СППР — это человеко-машинная информационная система, используемая для поддержки действий лица, принимающего решение (ЛПР) в ситуациях выбора, когда невозможно или нежелательно иметь автоматическую систему представления и реализации всего процесса оценки и выбора альтернатив. Во-первых, такие системы выступают в роли помощника лица, принимающего решение (ЛПР), который позволяет расширить его способности, но не заменяет его мнение и систему предпочтений. Во-вторых, они предназначены для использования в ситуациях, когда принцип принятия решения ввиду необходимости учета субъективного мнения ЛПР не может быть полностью формализован и реализован на ЭВМ.» Таким образом, в настоящем исследовании СППР строится в целях анализа данных и знаний, применяемых в процессе разыгрывания оптимизационной модели региональной транспортной инфраструктуры в контексте решения задач пространственной экономики.
Предлагаемая методика формализации данных и построения СППР
Как отмечалось выше, ранее в исследовании [1] построена многоуровневая модель оптимизации транспортной сети на базе гиперграфа транспортной системы (рис. 1). Она учитывает взаимосвязь географических особенностей исследуемого полигона, расположенной на нем транспортной сети и расположенной на том же полигоне пространственно-локализованной экономической системы, что в свою очередь также является критериями оптимизации.
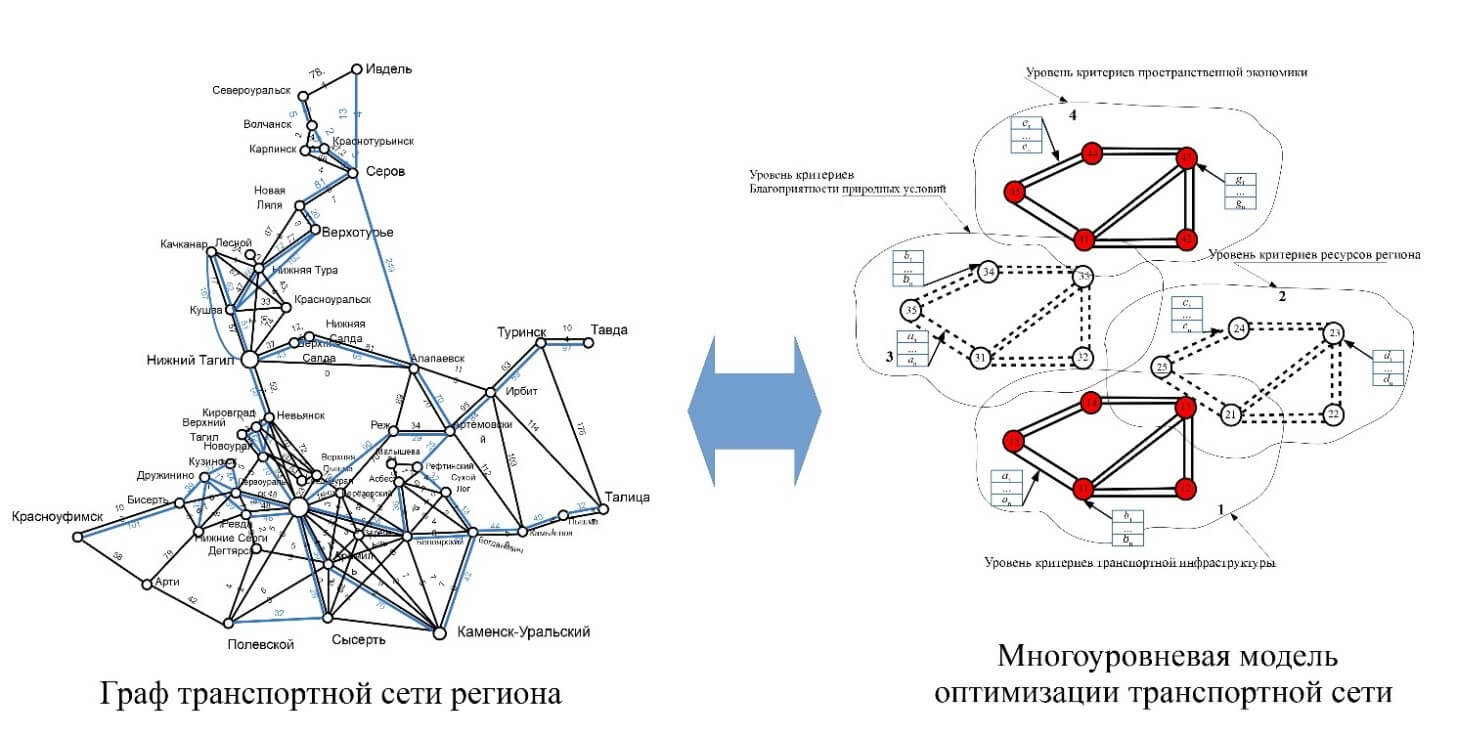
Рис.1 – Схематическое изображение алгоритма методики многокритериальной оптимизации
Реализация модели обеспечена методами векторной оптимизации. При выборе критериев и построении векторов оптимизации были определены факторы основанные на данных и знаниях смежных научных отраслей. Однако при свойственных разработанной методике преимуществах в процессе исследования стало очевидно, что примененный подход предъявляет высокие требования к качеству априорных данных и знаний используемых в процессе моделирования. В частности, уже на начальном этапе нужно знать какие критерии влияют на оптимальность системы, из каких факторов эти критерии состоят и вообще, что понимается под оптимумом для данной системы и на какой продолжительности ее жизненного цикла эта оптимальность может сохраняться. Успешность моделирования в таком случае сильно зависит от квалификации привлеченных до начала моделирования экспертов, качества и полноты информации и других обстоятельств, которые не предопределены. В связи с указанными обстоятельствами потребовалась доработка методтики, направленная на преодоление негативного влияния перечисленных факторов. Ниже представлены результаты исследования, усовершенствующие предложенную ранее методику.
Основным направлением совершенствования методики является построение СППР, которая позволит ЛПР в эвристическом процессе не только формализовать данные и генерировать информацию об исследуемой системе для последующей оптимизации на разработанной ранее модели, но и будет самостоятельным исследовательским инструментом. В качестве основы для создания базы данных СППР применен граф транспортной системы. В качестве методической основы – методы теории ситуационного управления.
Модель многокритериальной оптимизации хорошо работает в том случае, когда мы уже имеем статическое состояние формализованной и хорошо структурированной системы, для случая когда эти условия не выполняются необходимо применение дополнительных методов. В нашем случае применена семиотическая модель, которая позволяет гибко и вариативно работать с данными и информацией. Такимо образом, мы имеем возомжность проверить гипотезы, оперируя не только формализованной информацией, но и привлекая дополнительные данные и рассматривая новые состояния системы.
Рассмотрим семиотическую модель, в классической форме, как это приводится у Д.А. Поспелова [2].
М=<T, P, A, П> (1)
Т – множество базовых элементов, состоит из множества элементов любой природы (в нашем случае это ребра и вершины графов). Существует конструктивная процедура π1, которая позволяет установить одинаковы Tn и Tn+1 или нет. Процедура π2 позволяет установить принадлежит элемент T или нет.
Р – Синтаксические правила, используются для того, чтобы из базовых элементов строить такие их совокупности, которые в рамках данной формальной системы считаются синтаксически правильными совокупностями. На синтаксические правила нет особых ограничений, нужно только, чтобы была процедура π3, которая позволяла бы установить является эта синтаксическая совокупность правильной или нет.
А – Система аксиом, образует любое множество синтаксически правильных совокупностей. (в нашем случае это очень удобно, так как мы можем выделять любые интересующие нас элементы, в том числе кластеры и подграфы.)
П – Семантические правила или правила вывода, расширяют, если это возможно, множество аксиом, добавляя к ним новые синтаксически правильные совокупности (в нашем случае это важно, потому как позволяет соотносить междисциплинарные данные, а также организовать взаимоотношения данных на разных уровнях многоуровневой модели).
Множество после применения семантических правил и аксиом называется множеством семантически правильных совокупностей.
Формальная модель, для которой существуют конструктивные процедуры π1, π2 и π3 называется конструктивной формальной моделью.
Интерпретированная формальная модель
L=<Z, D, H, V> (2)
Z – множество интерпретируемых значений (в нашем случае это могут быть: протяженность, количество полос/путей движения, пропускная способность, средняя скорость на участке, вероятность безотказной работы. и др. )
D – правила отображения, устанавливают возможность T↔Z, эти правила при конкретной реализации дают отображение T→Z, т.е. приписывают каждому элементу из T интерпретирующее значение.
H – правила отображения задают те или иные реализации отображения или они задаются из вне (на данном этапе моделирования можно задавать самые разные в т.ч. функциональные зависимости, интересующие нас).
V – правила интерпретации позволяют приписывать любой синтаксически правильной совокупности базовых элементов некоторое интерпретирующее значение.
И, наконец, семиотическая модель
С=<M, xT,xP,xА,xП> (3)
Все элементы, входящие в определение М (формальную модель) могут изменяться по следующим правилам:
xT,xP,xА,xП – правила изменения Т, Р, А, П, где
xT, — меняет синтаксис базовых элементов ,
xP – меняет синтаксис совокупностей базовых элементов (форма явления),
xА – меняет семантику (назначение явления в общем случае),
xП – меняет прагматику (значение явления в частном случае, т.е. в настоящий момент времени здесь и сейчас для ЛПР).
Адаптируя семиотическую модель для целей нашего исследования получим следующее. Пусть гиперграф (см рис. 1) многоуровневой модели задан формальной моделью М, где Т – элементы гиперграфа, однозначно определяемые и отличимые друг от друга с помощью правил Р, А – синтаксис элементов графа и П – правила его расширения. Исследователь (ЛПР) с помощью модели L интерпретирует эту модель в текущем состоянии М1 и далее проверяет различные гипотезы (см. рис.2), суть которых формулируется с помощью правил xi = <xT,xP,xА,xП>
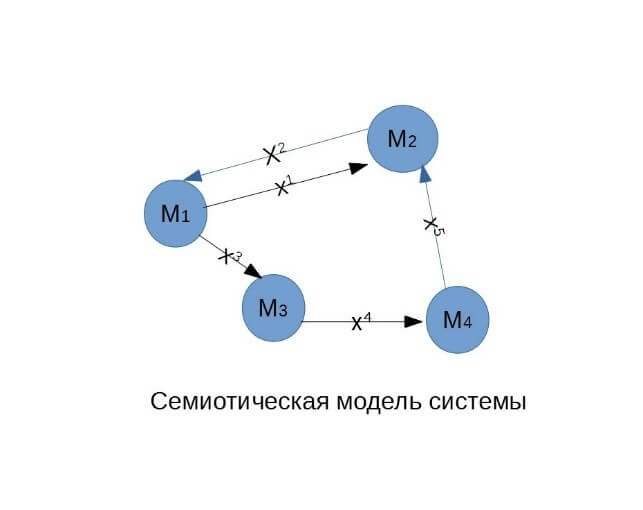
Рис. 2 – Проверка гипотез исследования с помощью адаптированной семиотической модели системы
Рассмотрим процесс проверки гипотез ЛПР (рис.2). Здесь следует отметить, что существует некоторое исходное состояние формальной модели М, которое соответствует текущему состоянию системы и уровню знаний о нем, что в практическом значении тождественно состоянию полной ситуации S. В нашем случае такому состоянию формальной модели соответствует полный гиперграф транспортной системы и все транспортные и экономические процессы, которые на нем происходят. С точки зрения информационных технологий этому состоянию соответствует полная база данных и знаний об исследуемом объекте, а также процедур, которые могут с ними выполняться. На каждом этапе исследования системы иметь дело с полной ситуацией не удобно и не всегда целесообразно. Переходы из одного состояния формальной системы Mi в Mi+1 связанные с изменением полной ситуации Si+1 имеют место в общем случае, но мы оставим их за скобками алгоритма, изображенного на рис. 2. В данном случае мы рассматриваем такие переходы, при которых каждому состоянию Mi соответствует состояние модели, для которого ситуация является полной только для условий, справедливых для проверяемой гипотезы. Таким образом, мы получили исследовательский инструмент, который формализует процесс разделения модели на уровни не в частном случае, как это делалось ранее в процессе многокритериальной оптимизации, когда выделялось четыре уровня, но в общей постановке, когда количество уровней и взаимосвязей между ними произвольно и определяется с помощью правил семиотической модели xT,xP,xА,xП. В практическом отношении это означает, что ЛПР получает возможность работать со структурой графа в привязке к его форме и составу, изменяя количество значимых в каждом отдельном опыте элементов графа, используя их как знаки, и присваивая им различные смысловые значения для получения новых данных и знаний об объекте.
Далее мы рассмотрим вопрос о том, что в настоящей методике понимается под проверкой ЛПР гипотез. В качестве гипотез в данном случае выступают ситуации и сценарии, которые позволяют применить к системе то или иное утверждение или изменение условий и получить новое соответствующее им отображение модели. Самым простыми примерами может служить построение изохрон, отображение «узких мест» графа. Для этого достаточно задать соответствующие правила интерпретации и отображения формальной модели. Например, если речь идет об изохронах, тогда Z – это время прохождения участка от начала отсчета изохрон до искомого пункта, D – правило включения элементов в участок, для которого определяется Z, H – сравнение текущего значения функции времени прохождения участка и нормативного значения, V – обозначение цветом элементов, для которых значения Z одинаковы (см. рис. 3). Но существуют и более сложные сценарии, которые уже не получиться сформулировать с помощью таких простых зависимостей, а они требуют выполнения более сложных алгоритмов и дополнительных методов реализации. Для таких случаев предлагаемой методикой предусмотрено применение фреймов [7].
М. Мински в [7] отсылает нас к проблеме мышления внутри парадигм и ее негативного влияния на объективность суждений, определяя фреймы, как один из инструментов объективизации знаний. Для нас это существенно важно потому, что ранее в исследовании мы ставили себе целью снизить степень такого влияния за счет междисциплинарной постановки проведения исследования, а, следовательно, выхода из рамок отраслевых парадигм науки, путем их взаимного анализа и синтеза. Качество результатов при таком подходе повышается за счет того, что выдвигаются и подвергаются проверке не только такие гипотезы, которые формируются внутри существующих парадигм и вытекают из привычной логики и хорошо зарекомендовавших себя теорий, но и такие которые становятся следствием поиска и всестороннего анализа максимально возможного объема данных и знаний. Инструменты фреймового представления знаний являются методами и механизмами достижения этой цели.
Согласно определению, которое находим у Минского [7]: «Фрейм представляет собой не одну конкретную ситуацию, а наиболее характерные, основные моменты ряда близких ситуаций, принадлежащих одному классу. Группы связанных между собой фреймов объединяются в системы, которые могут отражать действия, причинно-следственные связи, изменения понятийной точки зрения и т. д.» В нашем случае важно, что фреймы создаются с участием всех причастных экспертов и при этом нет жестких ограничений на фиксируемые закономерности, следовательно, каждый эксперт фиксирует существенные для решения поставленных задач данные и знания из области его компетенции.
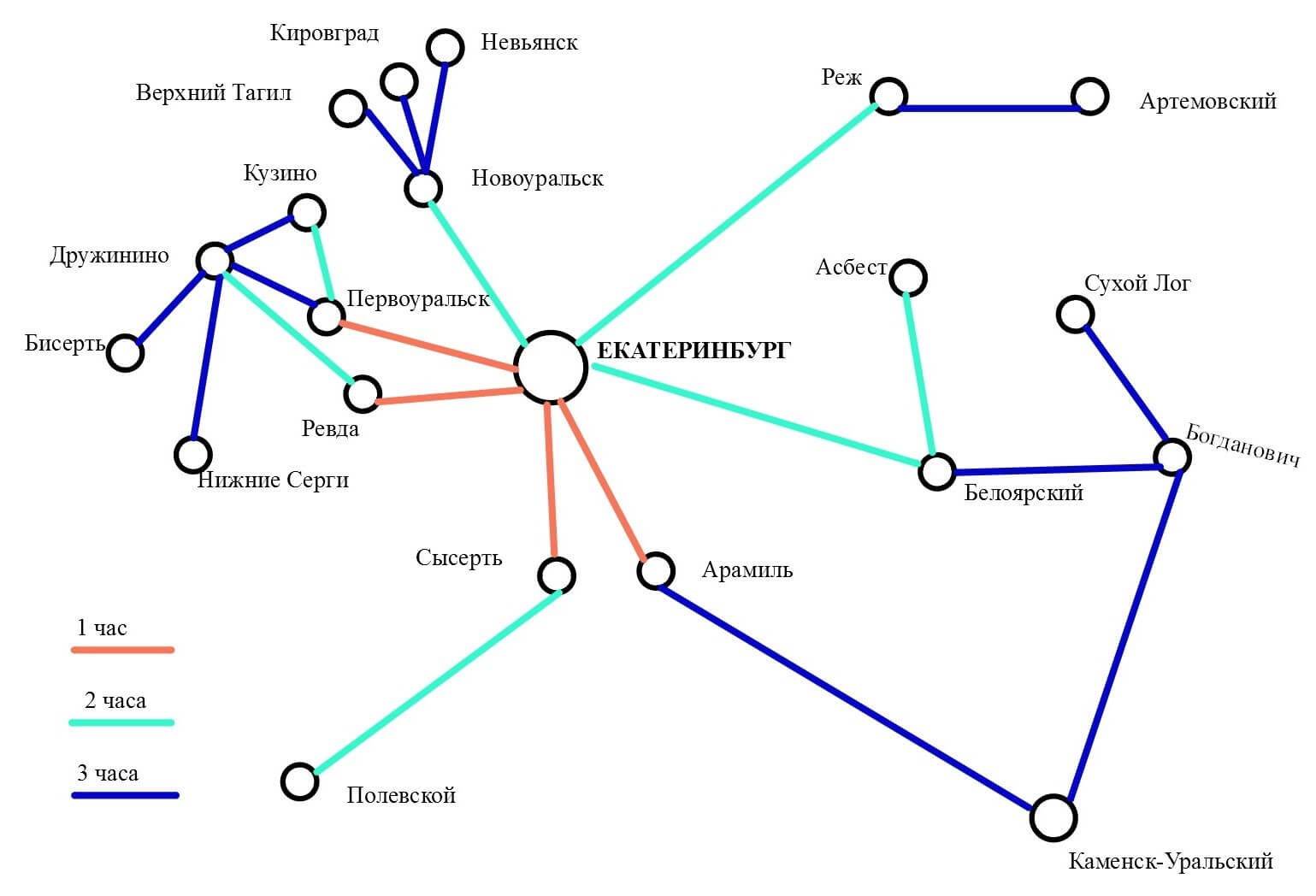
Рис. 3 – Отображение модели сети с изохронами пригородного железнодорожного пассажирского движения
Отличительной чертой фреймов от очень близких по смыслу процедур языков программирования будет наличие иерархии и наследования между фреймами. Благодаря структуре и свойствам фреймов, все многообразие данных, которое выявляется в ходе исследования, накапливается и структурируется, формируя связи и закономерности вне зависимости от их осознанности исследователем на данном этапе. Таким образом, неструктурированные данные и знания преобразуется в строгие формы, пригодные для дальнейшего использования в целях системного анализа и моделирования.
Рассмотрим примеры фреймов с помощью которых построена предлагаемая в исследовании СППР (рис. 4-5). На рисунке 4 приведен фрагмент структуры фреймов, описывающих элементы гиперграфа. В частности, показано как с помощью фреймовой модели решается задача о проверке возможности пропуска дополнительного объема грузов по участку железной дороги. Для этого кроме фрейма-структуры применяется фрейм-сценарий (рис. 5). На рисунке видно, что для исследуемого участка условия пропуска дополнительного объема выполнены. Аналогичным образом может быть решена задача о поиске «узких мест», если алгоритм применить ко всем ребрам гиперграфа.
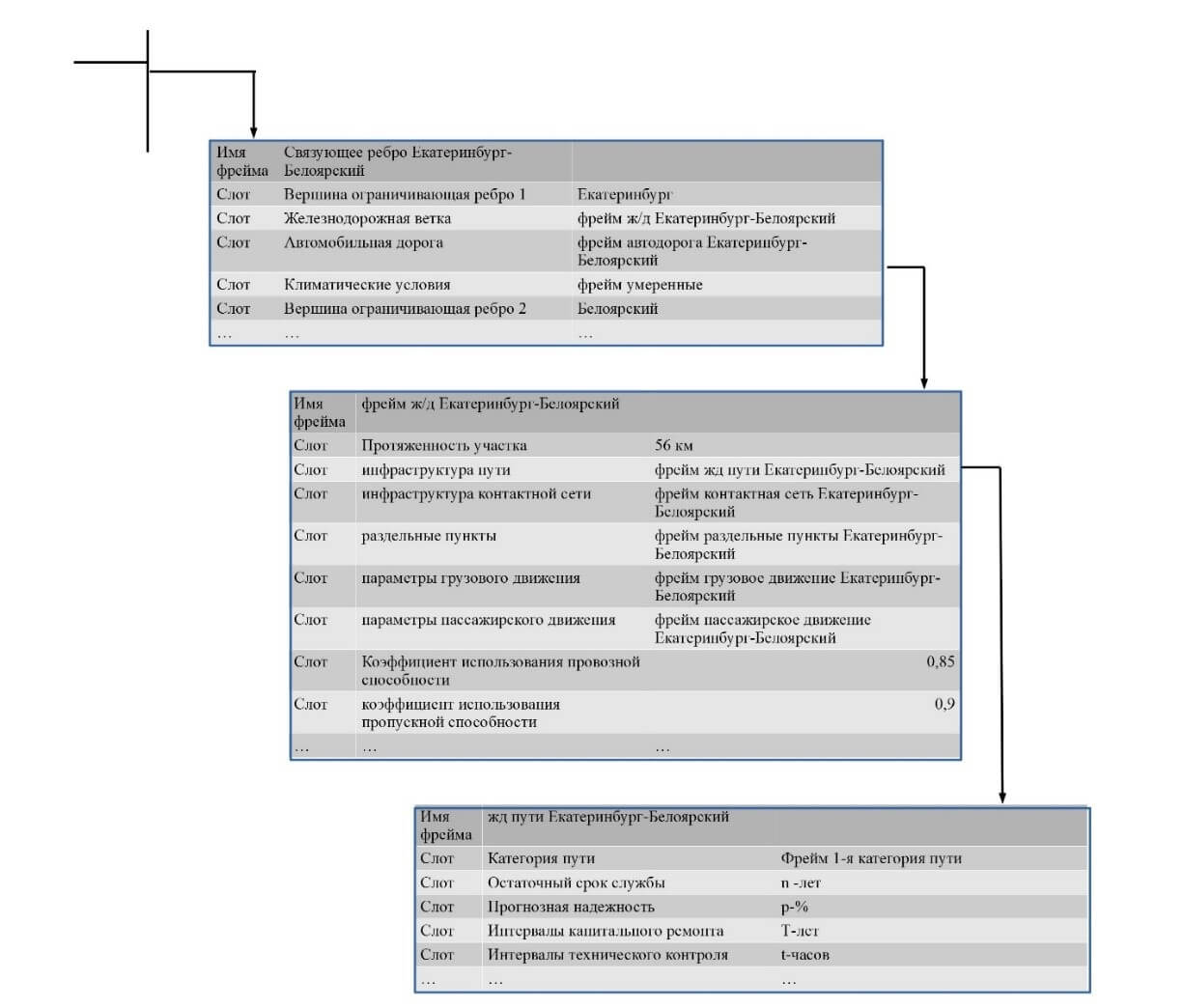
Рис. 4 – Пример фрейма-структуры, входящего в СППР
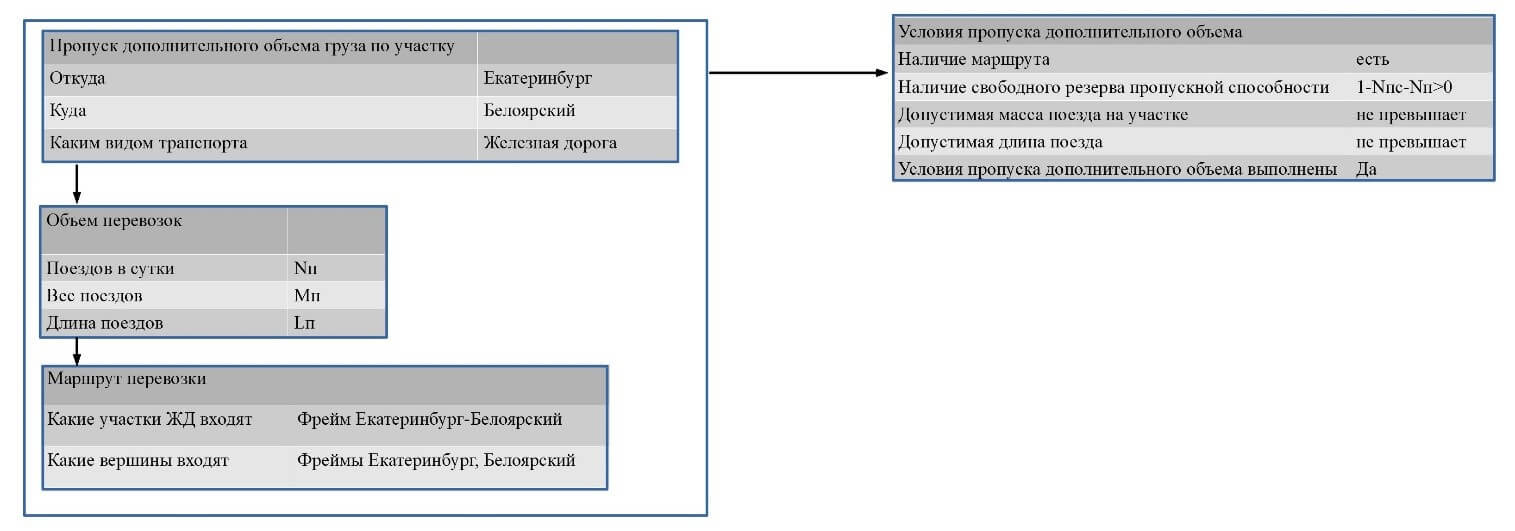
Рис. 5 – Пример фреймов-сценариев, входящих в СППР
Очевидно, что приведенные здесь примеры несут лишь демонстративный характер, иллюстрируя общий принцип работы методики. Вопросы и проблемы, представляющие реальный научный и практический интерес исследования, описываются с помощью фреймовых конструкций существенно большего объема. Применяемые здесь аппарат фреймов является универсальным для анализа практически любого вида данных, которые анализирует ЛПР, хотя и не лишены некоторых недостатков. Тем не менее при квалифицированном применении методов создания и обработки фреймовых моделей они доказали свою эффективность не только в нашем случае, но и при создании экспертных систем в том числе с применением искусственного интеллекта (ИИ). Это создает хороший задел для дальнейшего развития методики с помощью инструментов объектно-ориентированного программирования и систем ИИ.
Заключение
Результаты исследования дополняют предложенную ранее оригинальную методику оптимизации транспортной системы региона в рамках задачи формирования пространственно-локализованной экономической системы пространственной экономики. На первом этапе исследования была построена многоуровневая модель и предложены алгоритмы оптимизации транспортной сети с опорой на заранее определенные критерии оптимальности. При этом транспортная сеть является пространственным каркасом исследуемых экономических систем и реализует пространственные связи. Критериями оптимизации являются параметры транспортной сети, географические особенности исследуемого полигона, а также параметры систем пространственной экономики.
На втором этапе исследования, результаты которого представлены в данной статье, стояла задача повышения вариативности модели, путем дополнения методики оптимизации инструментами анализа слабо формализованных данных и декларативных знаний. В качестве результата планировался методический инструмент, позволяющий достичь эффекта взаимного проникновения данных и знаний из смежных отраслей науки и оценки их взаимного влияния на результат исследования. В связи с указанными обстоятельствами были применены адаптированная семиотическая модель и фреймовая модель представления знаний.
Применение адаптированной семиотической модели дает широкие возможности в многовариантном отображении гиперграфа с осуществлением вертикальной иерархии модели (выделение слоев: транспортного, географического, экономического), а также горизонтальных связей (выделение подграфов, кластеров, осей). Кроме того, формулирование семиотической модели приводит данные к виду, удобному для перевода на языки программирования ЭВМ, работающие в ситуационной постановке проблем. Механизмы интерпретации семиотической модели позволяют уйти от узкой оптимизационной модели к более широкому анализу информации представленной в виде символов и декларативных знаний.
Применение фреймовой модели знаний является инструментом формализации и структурирования данных, с помощью которых решаются задачи ситуационного управления. В данном случае под ситуациями понимаются различные сценарии и алгоритмы, выступающие в качестве гипотез, служащих для получения априорных данных оптимизационной модели и решения ее подзадач, а также самостоятельные задачи, постановка которых в оптимизационном виде неправомочна.
Совокупность семиотической и фреймовой модели формируют собой СППР, развитие которой и совершенствование в виде программного продукта имеет высокий потенциал не только как составная часть предложенной здесь методики, но и как самостоятельный инструмент для решения практических задач проектирования и управления экономических и транспортных системам, локализованных на инфраструктуре транспортной сети региона.
Список литературы
- Маслов А.М. Основные положения методики оптимизации транспортной инфраструктуры в рамках формирования пространственно-локализованной экономической системы// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №4 (48). Номер статьи: 4836. Дата публикации: 2016-12-14. Режим доступа: https://eee-region.ru/article/4836/
- Поспелов Д.А. Ситуационное управление: теория и практика. М.: Наука, 1986. — 288 с.
- Клыков Ю.И. Ситуационное управление большими системами. М.: Энергия, 1974. — 136 с.
- Клыков Ю.И. Семиотические основы ситуационного управления. М.: МИФИ, 1974. — 220 с.
- Филиппович А. Ю. Интеграция ситуационного, имитационного и экспертного моделирования в полиграфии. М., 2003. — 310 с.
- Аксенов К.А. Моделирование и принятие решений в организационно- технических системах: учебное пособие. В 2 ч. Ч. 1 / К. А. Аксенов, Н. В. Гончарова. – Екатеринбург: Изд-во Урал. ун-та, 2015. – 104 с.
- Минский М. Фреймы для представления знаний – М.:Энергия, 1979 – 152 с.
References
- Maslov A.M. The main provisions of the methodology for optimizing the transport infrastructure within the framework of the formation of a spatially localized economic system [Osnovnye polozhenija metodiki optimizacii transportnoj infrastruktury v ramkah formirovanija prostranstvenno-lokalizovannoj jekonomicheskoj sistemy]// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — № 4 (48). Number of article: 4836. Date of publication: 2016-12-14. Access mode: https://eee-region.ru/article/4836/
- Pospelov D.A. Situational management: theory and practice [Situacionnoe upravlenie: teorija i praktika]. М .: Science, 1986. — 288 with.
- Klykov Ju.I. Situational management of large systems [Situacionnoe upravlenie bol’shimi sistemami]. M .: Energia, 1974. — 136 p.
- Klykov Ju.I. Semiotic basis of situational management [Semioticheskie osnovy situacionnogo upravlenija]. Moscow: MEPhI, 1974. — 220 p.
- Filippovich A. Ju. Integration of situational, simulation and expert modeling in polygraphy [Integracija situacionnogo, imitacionnogo i jekspertnogo modelirovanija v poligrafii]. M., 2003. — 310 p.
- Aksenov K.A. Modeling and decision making in organizational and technical systems [Modelirovanie i prinjatie reshenij v organizacionno-tehnicheskih sistemah]: a manual. At 2 pm Part 1 / K. A. Aksenov, N. V. Goncharova. — Ekaterinburg: Publishing house Ural. University, 2015. — 104 p.
- Minskij M. Frames for the representation of knowledge [Frejmy dlja predstavlenija znanij].- M.: Energy, 1979 — 152 p.
Еще в рубриках
Свердловская область
Региональная экономика