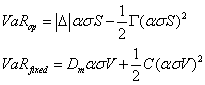Развитие методов VaR для оценки рисков на финансовых рынках
Development of methods of VaR for risk assessment in financial markets
Авторы
Аннотация
Впервые идея о необходимости управления рисками возникла вследствие череды крупных финансовых крахов в начале 1990 годов таких компаний как Orange Country, Barings, Metallgesellschaft, Daiwa и многих других. Общим выводом из этих событий стало осознание факта, что огромное количество денег может быть потеряно вследствие слабого контроля и управления финансовыми рисками. Поэтому многие финансовые институты инициировали начало исследований в этой области.
Ключевые слова
управление рикшами, финансовые риски, финансовые институты, финансовый кризис, регион
Рекомендуемая ссылка
Развитие методов VaR для оценки рисков на финансовых рынках// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №4 (8). Номер статьи: 801. Дата публикации: 27.12.2006. Режим доступа: https://eee-region.ru/article/801/
Authors
Abstract
The idea of the necessity of risk management has arisen as a result of a succession of large-scale financial failures in the early 1990s, companies such as Orange Country, Barings, Metallgesellschaft, Daiwa and many others. The general conclusion from these events was to realize that a huge amount of money can be lost due to poor control and management of financial risks. Therefore, many financial institutions have initiated the beginning of research in this area.
Keywords
management of rickshaws, financial risks, financial institutions, financial crisis, the region
Suggested Citation
Development of methods of VaR for risk assessment in financial markets// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №4 (8). Art. #801. Date issued: 27.12.2006. Available at: https://eee-region.ru/article/801/
Впервые идея о необходимости управления рисками возникла вследствие череды крупных финансовых крахов в начале 1990 годов таких компаний как Orange Country, Barings, Metallgesellschaft, Daiwa и многих других [1, стр. 35-46]. Общим выводом из этих событий стало осознание факта, что огромное количество денег может быть потеряно вследствие слабого контроля и управления финансовыми рисками. Поэтому многие финансовые институты инициировали начало исследований в этой области. Ключевым моментом в истории риск-менеджмента стала публикация в октябре 1994 года компанией JP Morgan технического документа, который с тех пор дорабатывался и улучшался уже несколько раз.
1. Введение в VaR
Инвесторам необходима методология для определения и измерения рисков, которые на финансовых рынках определяется как степень неопределённости будущих доходностей. Для этой цели всегда необходимо понимать природу возникающих рисков. Технический документ JP Morgan предлагает одну из возможных классификаций рисков, основанную на источнике возникающей неопределённости:
- Кредитные риски оценивают возможные потери вследствие невозможности другой стороны выполнить свои обязательства
- Операционные риски происходят от ошибок, которые могут быть сделаны во время обеспечения сделок – приема платежа или задание параметров банковских транзакций
- Риски ликвидности отражают потенциальную неспособность компании обеспечить выполнение обязательств вследствие неликвидности активов.
- Рыночные риски отражают неопределённость будущих доходов, связанную с изменением рыночных показателей (цены активов, процентных ставок, и т.д. )
До получения любых численных оценок риска, очевидно, инвестору сначала необходимо определить, с какими именно рисками он имеет дело, на практике также принимая во внимание необходимость компромисса между точностью модели и сложностью её реализации (как программной части, так и вычислительного комплекса).
Введем определение VaR. Согласно техническому документу RiskMetrics, Value-at-Risk – это мера максимального потенциального изменения стоимости портфеля финансовых инструментов с определённой вероятностью на заданном временном горизонте [2, стр. 6-7].
В общем случае, для получения этой величины необходимо ответить на 2 вопроса: 1 — какой объем активов потенциально рискован и 2 — каков этот риск в численном выражении (то есть, какие составляющие риска необходимо учесть и что является мерой этих рисков). Для простоты предположим, что инвестор заинтересован только в оценке рыночных рисков.
Для ответа на первый из поставленных вопросов, необходимо найти рыночную стоимость оцениваемых активов в основной валюте (откалибровать по рынку). Переход к количественному показателю риска требует оценки того, как сильно это рыночная стоимость может измениться. В финансах риск определяется как среднеквадратическое отклонение исторических доходностей от среднего уровня вследствие изменений в финансовых переменных [1, стр. 81].
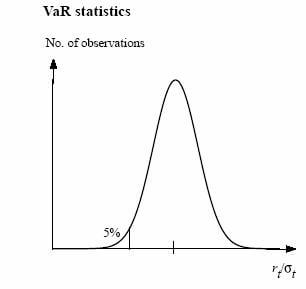
Далее, исходя из предположения, что нормированные доходности 
финансового инструмента распределены нормально с найденным значением среднеквадратического отклонения, при доверительном уровне 95%, VaR вычисляется как 
(рис. 1.1).
2. Методы вычисления VaR
Value at Risk стал важной составляющей набора инструментов риск – менеджера и инвестора, так как он дает численную меру риска. На практике, как правило, задача ставится не только получить достаточно точную оценку риска, но и оптимизировать затраты на её вычисление. Это подразумевает работу по выбору метода, который будет более подходящим для конкретного портфеля финансовых инструментов. В этой связи было разработано несколько подходов к оценке VaR.
Эти подходы к оценке VaR могут быть разделены на две группы. Первая группа использует локальные способы оценки. Эта группа измеряет риск через первоначальное определение стоимости в начальный момент времени, а затем использует производные для определения возможных изменений. Дельта-нормальный метод использует лишь линейную составляющую динамики через производную первого порядка или дельту (отсылаем читателя к греческим обозначениям в теории опционов) и подразумевает нормальность будущих распределений доходностей. Таким образом, метод дельта представляет собой аналитическую аппроксимацию производных первого и второго порядков и наиболее подходит для портфелей с ограниченным потенциалом риска.
Вторая группа методов использует так называемую полную оценку. Эти методы измеряют риск, полностью переоценивая портфель для каждого из широкого набора возможных сценариев. Методы полной оценки могут быть реализованы через метод исторического моделирования и метод моделирования Монте-Карло.
Эта классификация отражает фундаментальный баланс между скоростью, простотой реализации и точностью модели. Скорость становится очень важным параметром для больших портфелей из нескольких тысяч инструментов, подверженных многообразным рискам, обрабатывая также взаимодействие рисков через коэффициенты корреляций. В таких ситуациях, как правило, используется менее точный, но более быстрый дельта-нормальный метод. Точность, тем не менее, может быть более важным параметром, когда портфель содержит нелинейные компоненты.
2.1 Дельта-нормальная оценка
Методы локальных оценок обычно основываются на предположении о нормальности распределений доходностей. Это предположение особенно удобно, так как в этом случае сумма нормально распределенных переменных сама является нормально распределенной величиной.
Чтобы проиллюстрировать этот подход, необходимо выбрать инструмент, стоимость которого зависит лишь от единственного лежащего в основе фактора риска – цены S базового актива, входящего в портфель. Первый шаг состоит в оценке начальной стоимости портфеля
Определим 
как частную производную первого порядка, или, иначе, как чувствительность портфеля к изменению цены актива. В финансовой литературе [3, 4] эта производная называется модифицированной дюрацией для портфеля из инструментов с фиксированной доходностью или дельтой для деривативов [3, 5].Таким образом, потенциальная потеря стоимости, 
, может быть вычислена следующим образом:
Если распределение доходностей нормальное, значение VaR для портфеля может быть получено как произведение размера актива на VaR базового актива портфеля:
где 
— это коэффициент, соответствующий определенному уровню значимости (1.65 для 95%, 2.32 для 99%) и 
— среднеквадратическое отклонение возможных изменений стоимости базового актива. Этот метод оценки называется аналитическим. Для финансового инструмента с фиксированной доходностью, фактором риска является доходность 
и соотношение цена/доходность. В этом случае, VaR (рисковая стоимость) инструмента находится следующим образом:
, где 
— модифицированная дюрация облигации.
Среди достоинств дельта-нормальной оценки выделяется простота реализации и быстрота вычислений даже для очень большого количества финансовых активов, входящих в портфель, так как эта оценка заменяет каждую позицию в портфеле её линейной аппроксимацией.
Основным недостатком этого метода является недооценка значений, которые не описываются нормальным распределением доходностей (толстых хвостов распределений Леви) и, в некоторых случаях, неадекватное описание поведения нелинейных финансовых инструментов, таких как ипотечные бумаги.
2.2. Дельта-гамма оценка (оценка через «греческие символы»)
или, используя финансовые обозначения,
где 
— модифицированная дюрация и 
— коэффициент при производной второго порядка, называемая конвекцией. В предположении о нормальности, аналитическая формула для рисковой стоимости достаточно проста и для нелинейных инструментов (в частности, опционов), и для инструментов с фиксированной доходностью:
Существует также большое количество дальнейших развитий аналитических методов, корректирующих значение рисковой стоимости (VaR) в соответствии со значениями производных более высокого порядка, таких, например, как метод Корниша-Фишера [1]. Но эти подходы нивелируют основное преимущество аналитических методов, требуя все больших вычислительных ресурсов.
Ещё одним способом улучшения точности оценки является так называемый дельта-гамма-Монте-Карло метод, в рамках которого генерируются случайные реализации риск – факторов 
, с дальнейшей подстановкой полученных значений в приближение Тейлора для получения возможных сценариев движений исследуемого актива. Этот метод также известен как метод частичного моделирования [1, 2]. Эти изощренные методы могут быть использованы для более точной настройки параметров скорости и точности у системы оценки рисковой стоимости.
Преимущества и недостатки оценки методом дельта-гамма похожи на те, которые были отмечены выше для дельта-нормального метода. На самом деле, используя этот подход можно улучшить точность вычислений и учесть нелинейный вклад в приближение, но в то же время, значительно увеличивается трудоемкость вычислений.
2.3. Методы полной оценки (Монте-Карло)
В некоторых ситуациях способ аппроксимации через разложение в ряд Тейлора не подходит совсем. К примеру, в случае, когда наихудшие потери не могут быть получены при экстремальных изменениях базисных активов, как это происходит для длинного стрэддла (long straddle), когда покупаются одновременно опционы типа «пут» и типа «колл» с одинаковыми страйковыми ценами и сроками исполнения в расчете на неустойчивость конъюнктуры. Максимальная потеря, являющаяся суммой уплаченных премий по опционам, достигается в случае, когда цена базисного актива вообще не изменяется.
В этом случае используется метод полной оценки, рассматривающий стоимость портфеля для широкого значения возможных ценовых изменений:
Новые значения 
могут быть сгенерированы с помощью методов статистического моделирования, в частности, метода Монте-Карло, который основывается на априорном задании распределения возможных приращений. Другим способом получения значений 
может стать метод исторического моделирования, который просто создает выборку из недавних исторических значений. А именно, возвращаясь к прошлым значениям, применяет определенные веса к временному ряду исторических значений доходности. Этот подход иначе называется бутстрэппингом, или использованием существующего варианта процесса для создания нового варианта, так как предусматривает использование распределения недавних исторических значений [1].
В обоих случаях формируется стоимость портфеля на заданную дату, используя метод полной оценки. Этот метод потенциально является самым точным, так как он учитывает все возможные нелинейности и даже всевозможные выплаты, которые обычно просто игнорируются при применении дельта-нормального подхода. Подход VaR в методе полной оценки вычисляется из требуемых перцентилей полного распределения возможных выплат. С точки зрения вычислительных процессов, этот подход достаточно требователен к ресурсам, так как необходимо полностью рассчитывать рыночную стоимость позиции для большого количества возможных изменений базисных активов – факторов риска.
С целью уменьшения требуемой интенсивности вычислений, иногда используется сеточный метод Монте-Карло [6], когда вычисление стоимости портфеля происходит не на всем множестве значений, а лишь на ограниченном количестве узловых точек [7].
Основным преимуществом метода исторического моделирования является возможность получения полной оценки достаточно простым методом в случае портфелей с большим количеством разнообразных инструментов и на короткие временные интервалы. Все, что требуется – это временной ряд агрегированных доходностей портфеля. Метод может учитывать все нюансы, также предоставляя возможность выбирать необходимый временной горизонт.
С другой стороны, метод исторического моделирования имеет ряд недостатков. Первый заключается в необходимости иметь достаточное количество исторических данных по динамике цен. Чтобы получить 1000 независимых значений моделирования 1-дневного изменения цены, требуются исторические данные за 4 года. В то же время, некоторые финансовые инструменты могут иметь более короткую историю. Вторым недостатком является тот факт, что используется только один из возможных вариантов развития событий. Другими словами, подразумевается, что прошлое полностью представляет будущее, что, вообще говоря, неверно. Если в окно не попали важные события, распределение будущих доходностей не будет хорошо представлено. И наоборот, выборка может содержать события, которые заведомо не повторятся в будущем.
Что касается метода Монте-Карло, то это наиболее мощный метод, который может, в принципе, учитывать широкий круг возможных рисков, включая, конечно, и нелинейные эффекты. Моделирование методом Монте-Карло может учитывать изменение волатильности во времени, толстые хвосты распределений и даже экстремальные сценарии развития событий. Моделирование восстанавливает полностью плотность вероятности данных и может быть использовано для проверки ожидаемых потерь после использования VaR.
Важнейшим недостатком метода Монте-Карло является большое время вычислений. Скажем, для портфеля из 1000 ценных бумаг, для каждой из которых генерируются 1000 дневных данных, общее число моделируемых чисел уже составляет 106. Кроме того, если процесс оценки стоимости актива также требует моделирования, полный вычислительный процесс становится слишком сложным для его выполнения в on-line режиме. Более того, ежедневные оценки VaR должны быть получены до открытия рынка на следующий день, то есть за несколько часов.
Метод моделирования Монте-Карло, кроме того, самый «затратный» в смысле требований к инфраструктуре и интеллектуальным ресурсам. Другим недостатком этого метода является зависимость от стохастического процесса при моделировании риска. В самом деле, метод Монте-Карло зависит от определенного стохастического процесса для базисных факторов риска также как модели ценообразования для опционов или ипотечных инструментов. Чтобы проверить, робастны ли полученные результаты к изменениям модели, результаты моделирования должны быть дополнены неким анализом чувствительности. Наконец, рисковая стоимость, оцененная через смоделированные данные, зависит от дисперсии выборки. Например, это случай, когда риск-факторы совместно нормальны и все выплаты линейны. В этом случае дельта-нормальный метод даст корректную оценку за один шаг. Тем не менее, в целом этот метод, вероятно, является наиболее полным подходом к измерению рыночных рисков, если моделирование производится, в определенном смысле, корректно.
3. Сравнение эффективности представленных методов оценки
| Метод |
95% VaR |
99% VaR |
| Дельта-нормальный Равные веса, ширина окна: |
||
| 50 дней |
95.1% |
98.4% |
| 250 дней |
95.3% |
98.4% |
| 1250 дней |
95.4% |
98.5% |
| Дельта-нормальный Экспоненциальные веса при: |
||
 |
94.7% |
98.2% |
 |
95.0% |
98.4% |
 |
95.4% |
98.5% |
| Историческое моделирование Ширина окна: |
||
| 125 дней |
94.4% |
98.3% |
| 250 дней |
94.9% |
98.8% |
| 1250 дней |
95.1% |
99.0% |
Средний столбец показывает, что все методы дают значения очень близкие к идеальному значению доверительного уровня в 95%. При значении уровня 99%, тем не менее, дельта-нормальный подход незначительно, но недооценивает рисковую стоимость. В упомянутом исследовании также сообщается, что значения VaR, полученные с помощью дельта-нормального подхода должны быть увеличены на 9-15%, чтобы добиться корректного покрытия (учесть наличие толстых хвостов).
Особенно отметим, что когда значение VaR превышается некоторым событием, это событие, в среднем, в 1.3-1.4 раза выше, чем мера риска, и показывает существенную недооценку риска. Этим эмпирическим анализом, однако, проверялись позиции с линейной структурой риска.
Что касается портфеля, состоящего из опционов, результаты исследований, приведенные в таблице 2, наглядно демонстрируют вышесказанное.
Таблица 2 — Точность и скорость различных методов вычисления VaR: 99% VaR портфеля опционов
| Метод |
Точность. Средняя абсолютная ошибка (%) |
Скорость. Время вычислений, секунд |
| Дельта-нормальный |
5.34 |
0.08 |
| Дельта-гамма-нормальный |
4.72 |
1.17 |
| Дельта-гамма-Монте-Карло |
3.08 |
3.88 |
| Сеточный Монте-Карло |
3.07 |
32.19 |
| Монте-Карло |
0 |
66.27 |
Полученные результаты подтверждают сказанное выше. Дельта-нормальный метод, как и ожидалось, имеет самое большое значение и наименьшее время исполнения. С другой стороны, наиболее точный метод – это метод Монте-Карло, который практически полностью определил действительное значение VaR, но ценой времени вычислений, более 1 минуты. Все другие методы представляют собой компромисс между точностью и временем вычисления. Интересным вопросом для будущих исследований является проверка того, насколько хорошо будут работать эти приближения в контексте больших диверсифицированных портфелей банков? Учитывая быстро уменьшающуюся стоимость вычислительных мощностей, методы полной оценки вскоре могут избавиться от перечисленных выше недостатков. Другим перспективным способом преодоления недостатков методов полной оценки является использование систем распределенных вычислений, в частности, кластеров, не требующих дорогостоящей инфраструктуры для высокопроизводительных вычислений.
Литература:
- Jorion Ph., Value at risk: the new benchmark for managing financial risk – 2nd edition, McGrow-Hill, 2001
- RiskMetrics Technical Document – JPMorgan, 4th edition, December, 1996
- Sharpe W., et all, Investments – Prentice Hall International, Inc.,1997
- Fabozzi F., Bond markets, analysis and strategies – 3rd edition, Prentice Hall International, 1996
- Wilmott P., Derivatives: The theory and practice of financial engineering, — John Wiley & Sons, 1999
- Picoult E., Calculating Value at Risk with Monte Carlo simulation, — Risk Management for Financial Institutions, 1997
- Nicrosini, O. Introduction to the Monte-Carlo Method, — IUSS lectures, 2005
Еще в рубриках
Финансы регионов