Актуальность работы обусловлена созданием качественной системы организации управления и прогнозирования социально-экономического развития региона (субъекта РФ). Рассмотрены существующие проблемы и проведен анализ организации управления экономикой регионом в современных условиях. Сформирована математическая модель развития экономики региона в виде векторной задачи математического программирования. Модель построена на основе межотраслевого баланса и учитывает инвестиционные вложения в каждую отрасль экономики региона.
Методы решения векторной задачи основаны на нормализации критериев и принципа максимина (гарантированного результата). Практическая реализация модели показана на статистических данных отдельного региона (Приморского края). В результате решения мы сформировали прогноз по основным показателям развития экономики региона на год, а также в динамике (на несколько лет). Направлениями дальнейших исследований авторы видят в разработке более совершенного программного обеспечения и его использования в практике прогнозирования каждого субъекта РФ.

Организация управления, Моделирование, Прогнозирование, Экономика региона, Векторная оптимизация.

Relevance of work is caused by creation of qualitative system of the organization of management and forecasting of social and economic development of the region (territorial subject of the Russian Federation). The existing problems are considered and the analysis of the organization of management of economy by the region in modern conditions is carried out. The mathematical model of develop-ment of economy of the region in the form of a vector problem of mathematical programming is created. The model is constructed on the basis of interindustry balance and considers investment investments in each branch of economy of the region. Methods of the solution of a vector task are based on normalization of criteria and the principle a maximine (the guaranteed result). Practical realization of model is shown on statistical data of the certain region (Primorsky Krai). As a result of the decision we have compiled a forecast on the main indicators of economic development of the region for a year, and also in dynamics (for several years).
The directions of further researches authors see in development of more perfect software and its use in practice of forecasting of each territorial subject of the Russian Federation.

The organization of management, Modeling, Forecasting, Economics of the region, Vector optimization

Введение

В настоящее время в системе государственного и регионального управления основополагающими стали краткосрочные прогнозы. Это связано с возможностями прогнозирования в условиях нестабильной переходной экономики, при которых приемлемая точность прогнозов не обеспечивается. Эффективным инструментарием вариантного прогнозирования в данных условиях может быть информационное (статистическое) и математическое моделирование экономических систем, которое широко использовалось в работах зарубежных [18, 19,20], русских авторов [2, 3, 4, 13, 14,17]. Именно это направление рассматривается в данной работе, которая является дальнейшим развитием исследований авторов [5 — 10].

Целью данной работы  является анализ организации управления экономикой регионом в современных условиях. Формирование математической модели развития экономики региона в виде векторной задачи и разработка на ее основе методологии моделирования,  прогноза развития экономики  региона на несколько лет с учетом инвестиционных процессов для последующего формирования бюджета региона.

Для реализации поставленной цели в работе рассмотрена схема организации  управления экономики региона и представлена методология моделирования и прогноза развития экономики  региона на несколько лет, которая включает:

• построение модели развития региональной экономики в рамках в виде векторной задачи математического программирования, где качестве управляющих переменных выбраны отрасли экономики — их развитие составляет основную цель, ограничениями являются межотраслевой баланс, ресурсы и производственные мощности  региона [6, 7, 11];
• подсистему макроэкономического моделирования, на основе которой формируется прогноз развития экономики региона при условиях «что…, если…»); в блоке межотраслевого баланса выделяется подсистема, где конечный спрос формируется за счет инвестиций, вкладываемых в развитие отрасли, как на уровне фирмы, так и на уровне региона, государства; подсистема макроэкономического моделирования экономики региона опирается подсистемы информационного и программного обеспечения;
• подсистему информационного обеспечения (базу данных), которая сформирована исходя из функций и структуры задач системы национальных счетов в том числе: системы основных национальных счетов: счет производства, сводные счета доходов, счета продуктов, услуг и т.д.; показателей развития по отдельным секторам экономики региона: нефинансовые и финансовые предприятия, государственные учреждения, и т. д.;
• подсистему программного обеспечения направленную на разработку прогноза развития экономики региона, включающую три блока задач: построение модели развития экономики региона в виде векторной задачи линейного программирования; решение векторной задачи линейного программирования, основанное на нормализации критериев и принципе гарантированного результата [7, 9]; и третий блок непосредственно моделирование с учетом инвестиций.

Задача векторной оптимизации (модель экономики региона) решается в динамике на несколько периодов планирования, в итоге получаем макроэкономические показатели: прогноз валового объем продукции по отраслям региона (млн. руб.); прогноз прироста конечного спроса за счет инвестиций по отраслям; прогноз конечного спроса по отраслям; прогноз совокупного конечного спроса по отраслям региона; промежуточное потребление; инвестиции в прирост конечного спроса; ресурсы региона, промежуточные затраты, валовую добавленную стоимость, а также показатели второго уровня.

При практической реализации требования к функциям и структуре программного обеспечения могут быть сформулированы и согласованы с заказчиком при постановке задачи. Основным плановым документом социально-экономического развития региона является бюджет. Таким образом, результаты моделирования являются входной информацией для подсистемы – «Доходная часть бюджета региона» с формированием соответствующей документации.

1. Организация управления регионом

Исследование организации управления экономикой региона и межотраслевых связей, проведенное с позиций системного подхода и теории управления [7], показало, что управление регионом  осуществляется на двух уровнях экономики (управление предприятием, отраслью) и третий уровень — бюджетная сфера [6, 11], что и представлено на рис. 1.

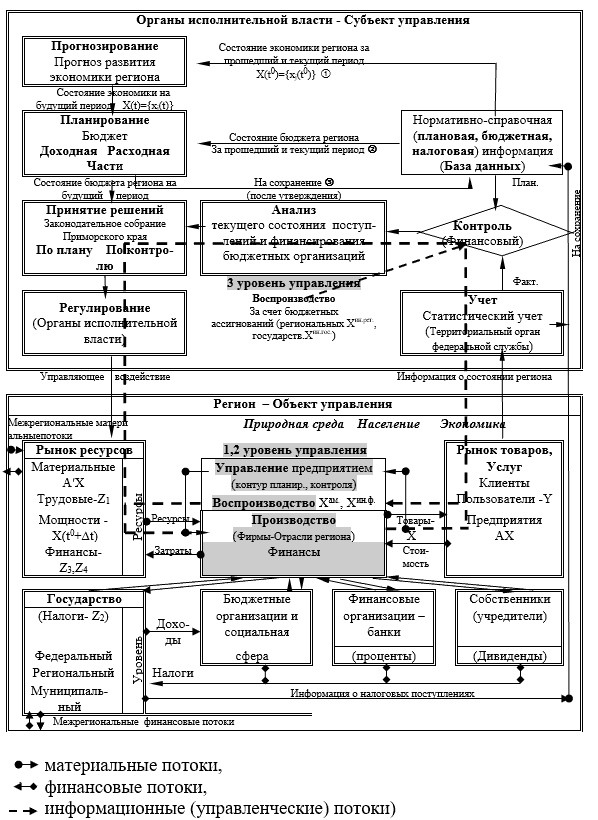
Рис. 1. Схема организации управления регионом

На уровне экономики региона управление реализуется рынком. Это связано с тем, что план производства того или иного товара определяется самим производителем (фирмой) и соответственно они же управляют объемами производства этого товара, с учетом возможного спроса, конкурируя между собой (внутриотраслевая конкуренция). Субъектом управления является руководство фирмой. Государство не оказывает влияние на номенклатуру и объемы выпускаемой продукции, т. е. со стороны государства осуществляется децентрализованное управление фирмой. В индивидуальности все фирмы образуют 1 уровень управления региона. Объединение предприятий, выпускающих однородную продукцию, представляет отрасль. Субъектом управления отрасли является соответствующий департамент (управление) в администрации региона. Множество подобных отраслей в совокупности создают  межотраслевую конкуренцию и образуют 2 уровень управления региона. Все предприятия (фирмы) и отрасли в совокупности образуют контур рыночного управления экономикой региона, что показано в нижнем блоке схемы организации управления регионом рис. 1. Объединение всех отраслей производства и реализации продукции представляет экономику региона, управления которой, как и экономикой отдельной фирмы децентрализовано. Но децентрализация не является полной, так как государство формирует налоговую политику, тем самым, определяя линию поведения каждой фирмы.  Таким образом, в основе управления номенклатурой и объемами производства всех товаров, циркулирующих в регионе, а также стремлением производителей получить, как можно высокую прибыль от реализации  этих объемов товара лежит механизм рыночной конкуренции (т. е. то, что называют «невидимой рукою» Адама Смита).

На уровне бюджета осуществляется управление социально-экономическим развитием региона, в рамках которого, в соответствии с теорией управления [7], регион разделен на два крупных блока: объект (природная среда, население, экономика региона) и субъект управления (решающий задачи планирования и контроля). Оба эти блока представлены на рис. 1. В общем, то считается, что такое управление и есть управление экономикой региона, хотя это есть лишь управление только бюджетной составляющей.   Действительно, статистические данные, представленные в табл. 1 (блок «Статистика») основными экономическими показателями за 2011, показывают, что в динамике объем валового регионального продукта (546552) более чем в пять раз превышает  доходы бюджета (109762).

Эти два уровня экономики и бюджета региона взаимосвязаны:

1. во-первых, (влияние уровня экономики на бюджет), при производстве и реализации товаров, произведенных в регионе, формируются налоговые отчисления, которые дают основу для доходной части бюджета региона, (а также доходной части бюджета муниципального образования и федерации).  Поэтому регион заинтересован в развитии экономики и увеличения доходной части бюджета. Следовательно, регион должен активно участвовать в управлении развитием экономики региона и влиять на объемы и номенклатуру выпускаемой продукции, и сохранять пусть даже обанкротившие предприятия. Для прогноза и оценки экономического потенциала региона, и, как следствие, налоговых поступлений,  формируется финансовый план, который в соответствии с бюджетным кодексом РФ [8] формируется на три года.  При разработке финансового плана используются статистические данные  развития экономики региона, (которые накапливаются в блоке «Территориальный орган федеральной службы по ПК» на рис. 1);
2. во-вторых, оценим влияние уровня бюджета на экономику, оно определятся тем, что на уровне бюджета наряду с другими формируются два мероприятия: расчет величины налоговых отчислений (к сожалению, как правило, на уроне государства);  формирование федеральных и региональных проектов (целевых программ).   Реализация этих мероприятий оказывает определенное влияние на развитие экономики региона, т. е. эти  мероприятия являются основными инструментами государственного регулирования и развития экономики региона.

2. Модель развития региональной экономики в рамках инвестиционного процесса

Построение модели развития экономики региона представим в виде векторной задачи линейного программирования. Для построения модели используем агрегированную модель экономики региона («отрасли — регион»), являющейся дальнейшим развитием модели, представленной в [6, 7, 10].

Введем понятие вектора переменных (управляющих переменных), критериев и ограничений, накладываемых на развитие экономики региона.

Вектор переменных. В его качестве примем:

X(t)={x_j(t), j=} – вектор-столбец, каждая компонента которого определяет валовой объем выпуска продукции j-го вида деятельности в t-ом периоде (t∈Т), показан на рис. 1, где n – множество видов деятельности на уровне разделов и подразделов, в соответствии с ОКВЭД [13], т.е. — это агрегированные виды деятельности, которые примерно соответствуют отраслям в старом понимании этого слова, Т – плановый период.

Y(t)={y_j(t), j=} – вектор-столбец, каждая компонента которого определяет конечное использование (конечный спрос) продукции j-го вида деятельности отрасли. Каждая компонента y_j(t) является составной частью вектора x_j(t). Для любой отрасли конечное использование y_j(t) определяется суммой конечного потребления y_j^пот(t), накопления y_j^нак(t) и чистого экспорта y_j^э(t):

y_j(t) = y_j^пот(t)+y_j^нак(t) + y_j^э(t) , j=.

I(t)={I_j(t), j=} – вектор-столбец, компонента которого определяет валовой объем инвестиций, вкладываемых в увеличение производственных мощностей.

В совокупности они определяют вектор переменных: X(t) ={X(t), I(t), Y(t)},

размерностью 3*n, который требуется определить на планируемый период.

Критерии. Цель развития региона определяется постоянным увеличением благосостояния каждого жителя региона, которое зависит от роста объема выпуска продукции каждого вида экономической деятельности (отрасли) и соответствующей заработной платой с одной стороны, и налоговых отчислений в бюджет государства с другой. Поэтому в качестве критерия примем максимум конечного использования (спроса) каждого вида продукции:

max Y(t) = {max y_j(t), j =}.

Для оценки региона в целом учитываются агрегированные показатели:

X^val(t)= — валовой (совокупный) региональный продукт, представляющий сумму валовых выпусков продукции; Y^val(t)=  — валовое конечное использование, представляющее сумму валового конечного использования выпусков продукции всех видов экономической деятельности.

В совокупности они представляет векторный критерий оптимизации:

Opt F(X,Y)= {max Y(t), max X^val(t), max Y^val(t)}.                                      (1)

Заметим, что векторная задача позволяет использовать и другие критерии отдельно или, добавляя их к векторному критерию, представленному в (1).

Ограничения. В модели экономики региона предусматривается три вида ограничений: балансовые, ресурсные и мощности.

• Балансовые ограничения вытекают из анализа межотраслевого баланса.

Валовой объем выпуска производящей отрасли равен сумме стоимостей продукции произведенной этой отраслью и переданной во все отрасли:

X_i(t) =a_ijX_j(t) + y_i(t), i=,                                                                    (2)   

где X_i – валовой выпуск продукции i-ой отрасли, a_ijX_j(t) — промежуточное потребление, a_ij – коэффициенты прямых затрат, полученных от i-го вида деятельности, на производство единицы продукции j-го вида деятельности.

Уравнения (2) называются балансами «выпуска».

Валовой объем выпуска потребляющей отрасли равен сумме материальных затрат на продукцию производимую в других отраслях и денежный доход от производства продукции:

X_j(t) =a_ij′ X_j(t)+z_j(t), j=,                                                                  (3)

где z_j(t) – денежный доход от производства продукции j-ой отрасли, включающей в себя заработанную плату z₁(t), налоги z₂(t), амортизацию z₃(t), прибыль z₄(t) и пр., т. е. z_j(t)=z_1j(t)+z_2j(t)+z_3j(t)+z_4j(t), j= — валовая добавленная стоимость j-го вида деятельности. Уравнения (3) — балансы «затрат».

В матричном виде эти ограничения примут вид:

X(t) = AX(t) + Y(t), X(t)=A′ X(t) + Z(t),                                                      (4)

где A = {a_ij, i,j=} – матрица прямых затрат.

• Ограничения по ресурсам. Обозначим r_ij – объемом затрат i-го ресурса на производство единицы продукции j-ой отрасли: R = {r_ij, j=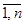, i =}.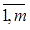

В целом ограничения примут вид:     RX(t) ≤ b(t⁰) + ∆b(t⁰ + ∆t),                (5)

где b(t⁰) = {b_i, i=} – объемы i-го ресурса, имеющегося в распоряжении региона на начальный период планирования t⁰∈T; ∆b(t⁰+∆t) = b(t⁰+∆t)-b(t⁰) – вектор приращений ресурсов, (t⁰+∆t), ∆t=0, 1, 2,…,Т.

• Ограничения по мощностям определяются как максимально возможные значения объемов производства X(t) (выраженные в денежных единицах) по всем видам экономической деятельности, которые лежит в пределах:

x_j(t⁰) ≥ x_j(t) ≥ x_j(t⁰+∆t), j=,                                                                     (6)

где x_j(t⁰) – объемы производства (объемы выполненных работ) j-го  вида деятельности в t⁰ (базовом); x_j(t⁰+∆t) – максимальные объемы производства, которые  j-й  вид может достичь на планируемый период времени (t⁰+∆t)∈T.

Региональная экономика направлена на повышения жизненного уровня населения региона — на увеличение продукции конечного использования (спроса – КС) всех видов деятельности региона, с учетом их воспроизводства на каждый период планирования. Эта целенаправленность можно выразить векторным критерием (1) при ограничениях по валовому объему выпуска производящей отрасли – межотраслевой баланс (2), по ресурсам (5) и мощностям (6), в совокупности они представляют векторную задачу линейного программирования:

Opt F(X, I, Y)={Y(t) = { max y_o(t), o=},                                             (7)

max Y^val(t)= y_v(t),    max X^val(t)= x_v(t)},                                              (8)

при ограничениях  (I—A)X(t)-VI(t) ³ Y(t),                                                       (9)

X(t)=(1-k^изн)X(t⁰) + φI(t),                                                                            (10)

RX(t) ≤ b(t⁰) + ∆b(t+∆t),                                                                            (11)

Tzmin≤R_trudX(t)≤Tzmax,                                                                            (11’)

X(t⁰) ≤ X(t) ≤ X(t⁰+∆t),       X(t⁰+∆t)=kX*X(t⁰),

I(t⁰) ≤ I(t) ≤ I(t⁰+∆t),          I(t⁰+∆t)=kinv*I(t⁰),

Y(t⁰) ≤ Y(t) ≤ Y(t⁰+∆t),        Y(t⁰+∆t)=kY*Y(t⁰),      t⁰+∆t= t⁰, t⁰+1, …, t⁰ +T,  (12)

где X(t)={X(t)={x(t), j=}, I(t)={I(t), j=}, Y(t)={y(t), j=}} — вектор неизвестных, X(t) — валовые выпуски, I(t) — инвестиции для всех отраслей (видов деятельности) и Y(t) — конечное использование региона на t∈ T;

F(X, I, Y) – векторный критерий (7), имеющий множество K=n+2 критериев, Y(t)  критериев максимизации КС, критерия суммарного конечного спроса и валового выпуска регионального продукта в (8) соответственно;

(9) —  межотраслевые балансовые ограничения с учетом инвестиций;

(10) – блок воспроизводства выпуска продукции с учетом инвестиций;

(11) – ограничения по ресурсам, в т. ч. трудовые ресурсы (11’);

(12)- ограничения по производственным мощностям, инвестициям и КС. Задача (7)-(12) представляет векторную задачу линейного программирования являющейся математической моделью развития экономики региона на дискретный (планируемый) период ∆t=0, 1, …, T , с учетом воспроизводства ресурсов (в рамках инвестиционного процесса) в каждом периоде ∆t∈T.

Для решения задачи (7)-(12) используется алгоритм, основанный на нормализации критериев и принципе гарантированного результата.

Задача (7)-(12) решается в динамике с периодом один год, ∆t=0, 1, …, T.

В результате решения получим: точку оптимума:

X^o(t)={X^o(t)={x_v⁰(t), v=}, I^o(t)={I_v⁰(t), v=}, Y^o(t)={y_v⁰(t), v=}}, где

• X^o(t) — валовые выпуски, I^o(t) — инвестиции для всех отраслей (видов деятельности) и Y^o(t) — конечное использование региона t∈ T;
• конечное использование всех отраслей, измеренное в относительных единицах — λ_v(y_v⁰(t)), v=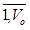, — такое измерение позволяет сравнивать развитие отраслей друг с другом: λ_v(y_v⁰(t))=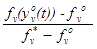, v=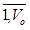, f_v^*— наилучшее решение задачи (7)-(12) по v-му критерию, f_v⁰— наихудшее решение по v-му критерию;
• λ^o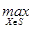(t)= λ(t)=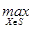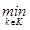λ_k(X(t)) – это максимальный уровень среди всех минимальных λ(t)= 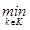λ_k(X(t)), ∀X(t)∈S на допустимом множестве S.  λ^o(t) также называют гарантированным результатом в относительных единицах, который гарантирует, что все отрасли, измеренные в относительны единицах,     λ_j(y_v⁰(t)) в точке оптимума {X^o(t), I^o(t), Y^o(t)} равны или больше λ^o(t), т.е. λ_v(y_v⁰(t)) ≥ λ^o(t), или λ^o(t) ≤ λ_v(y_v⁰(t)), v=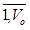, а в соответствии с теоремой 2, точка {λ^o(t), X^o(t), I^o(t), Y^o(t)} оптимальна по Парето;
• λ^o(t)=λ_v(y_o⁰(t)), v=, т. к. критерии (виды деятельности) (7) независимы, а для критериев (8), в оптимальной точке λ^o(t) ≤ λ_k(y_v⁰(t)), k=1, 2.

Полученная точка оптимума {X^o(t), I^o(t), Y^o(t)} дает возможность определить основные технико-экономические показатели региона, включенные в план, и соответствующие межотраслевые затраты: X_o(t)=a_ovx_o(t), ∀o∈ O.

Практическая реализация задачи (7)-(12) распадается на два этапа:

• построение численной модели региональной экономики;
• решение, последовательность действий в котором представляет методология моделирования развития региональной экономики.

3. Моделирование и прогнозирование развития экономики региона на базе статистических данных 2013 года (15 отраслей)

Механизм государственного регулирования экономики региона с использованием модели включает семь блоков:  1) анализ отчетных (статистических) данных за год  и построение на их основе межотраслевого баланса;

2) постановка задачи: формируется цель экономического развития и расчет коэффициентов динамической модели экономики  региона;

3) построение математической модели развития экономики региона в виде векторной задачи и формирование численной модели экономики региона;

4) процесс моделирования, в результате которого получим объемы валовых выпусков, конечного использования продукции отраслей региона на год;

5) формирование на годовой период показателей развития экономики региона, которые в совокупности представляют финансовый план региона;

6) прогнозирование развития экономики  региона в динамике — на трех летний финансовый план региона, в т. ч. налоговые отчисления, определяющие доходную часть бюджета региона одно — трех летний период;

7) принятие управленческого решения окончательного по развитию экономики региона — административное воздействие (регулирование).

3.1. Анализ статистических данных за год экономики региона

Анализ статистических данных, представленных основными экономическими показателями в табл. 1 в соответствии [11], характеризуют экономику региона в целом.

Таблица 1 — Объем и динамика валового регионального продукта

^{Источник: графы «Статистика» [11]; графы «Моделирование» — расчетные.}

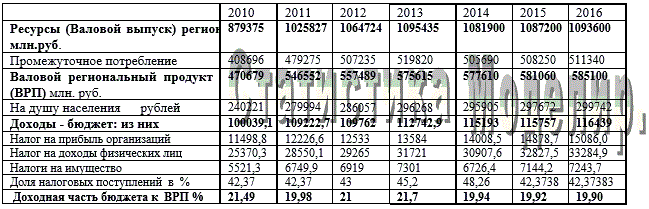
Базой для модельных построений использованы статистические данные:  «Счет производства по видам экономической деятельности» Приморского края за 2013 [11], представленные в табл. 2.

Экономические показатели: ресурсы (Валовой выпуск) региона, промежуточное потребление, валовой региональный продукт (ВРП) по состоянию на 2013 год разбиты на пятнадцать отраслей  [11] в соответствии с ОКВЭД [13].

Показатели табл. 2 перенесены в межотраслевой баланс табл. 4: ресурсы (валовой выпуск) Приморского края: {X_j(t), j=}, n=15 – представлены в 23 графе и 21 строке межотраслевого баланса; промежуточное потребление , где A_iX агрегированное промежуточное потребление  i= отрасли, 16 строка табл. 4; валовую добавленную стоимость: Z(t) – 20-я строка.

Таблица 2 — Счет производства по видам экономической деятельности в 2013 году

(в текущих основных ценах; млн.рублей)

Источник: [11]

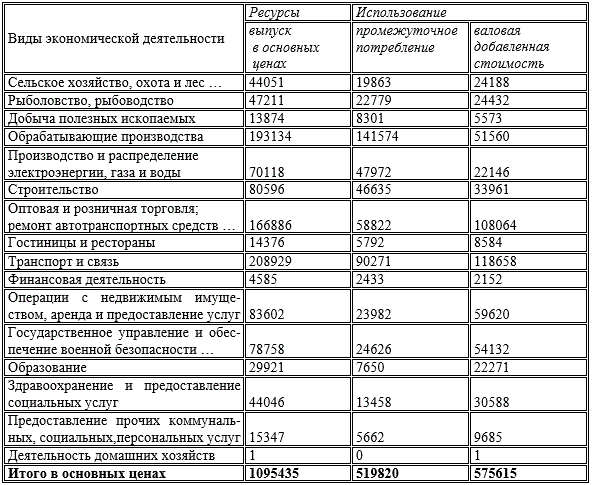
Расчет величин промежуточного потребления по всем видам экономической деятельности x_ij(t) , i=, j= произведен на основе процентной структуры межотраслевого баланса по РФ[1] по каждому виду экономической деятельности, которые представлены в табл. 3. Данные табл. 3 рекомендуется использовать только при первоначальной настройке программного обеспечения.

Таблица 3 — Структура промежуточного потребления межотраслевого баланса на 2003 г.

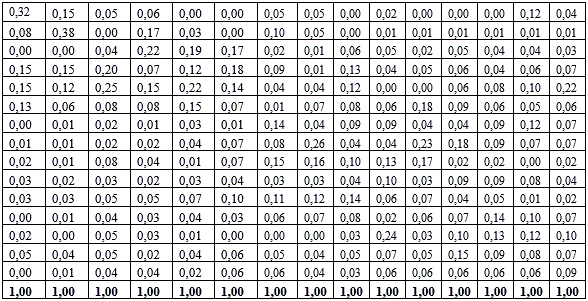
В дальнейшем, при реальных расчетах структура межотраслевого баланса по каждому региону может быть рассчитана на основе статистических данных, которые, согласно Распоряжению Правительства РФ [12] … о разработке базовых таблиц «затраты — выпуск» за 2011 год и последующие годы, и должны быть опубликованы на сайтах региона.

В 16 строке МОБ представлена сумма x_ij(t)’, j= — Итого промежуточное потребление. В 16 графе МОБ представлена сумма x_ij(t), i= — Итого промежуточный выпуск. Аналогично выполним расчет:

• конечного спроса — y_ij(t), i=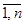, j=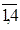, представленного в 17-21 графах:

Конечное потребление домашних хозяйств; Конечное потребление на коллективные услуги; Конечное потребление на индивидуальные услуги;  Валовое накопление основного капитала;  Изменение запасов материальных средств;  графа 22 — Итого конечный спрос;

• добавленной стоимости — z_ij(t), i=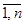, j=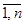 в 17-20 строках табл. 4: Оплата труда наемных работников; Другие налоги и отчисления; Валовая прибыль экономики и валовые смешанные доходы; Строка 21 — Валовая добавленная стоимость (сумма строк 17-20). Графа 23 — Всего ресурсов (валовой выпуск) сумма17 и 22 граф. Размерность матрицы межотраслевого баланса (21*23).

Таблица 4 — Межотраслевой баланс экономики региона (Приморского края за 2013 год), млн. руб.

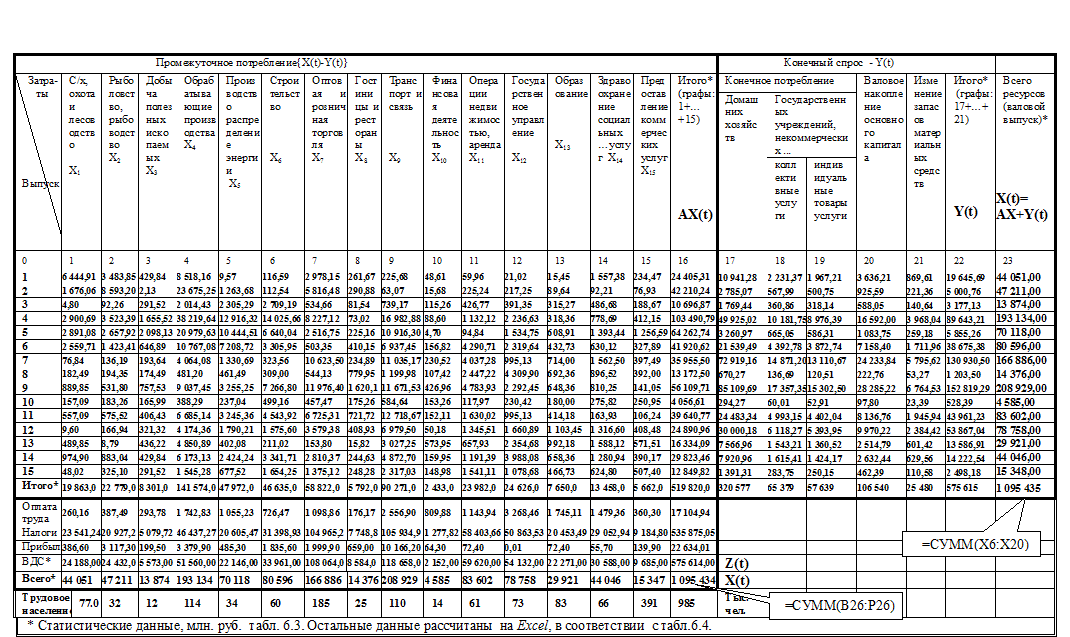
3.2. Расчет коэффициентов динамической модели экономики  региона  

Для построения численной динамической модели экономики региона (7)-(12) на основе модели матрицы межотраслевого баланса табл. 4, представленной в системе Matlab матрицей: Balans=, выполним расчет коэффициентов динамической модели, которые разделены на три блока:

1. проверка исходных данных;
2. расчет коэффициентов межотраслевого баланса;
3. построение коэффициентов инвестиций в  модели региона.

Блок 1. Проверка исходных данных включает следующие расчеты:

Итого промежуточной выпуск (сумма столбцов 1-15) – результат выдается в виде вектора-столбца (идентификатор AX), он должен совпадать с16-м столбцом;

Итого конечный спрос (сумма столбцов 17-21) – (идентификатор Y), он должен совпадать с 22 столбцом Y(t)={Y_ij(t), i=, j=22};

Итого промежуточное потребление (сумма по столбцам 1-15) – (идентификатор PromP_AX), он должен совпадать с 16 строкой;

Итого Валовой объем Х (сумма столбцов 16+22) – (идентификатор AX_Y), он должен совпадать с 23 столбцом;

Итого валовая добавленная стоимость (Сумма ВДС по строкам с 1 по 15 столбец) – (идентификатор SumZ2), он должен совпадать с 20 строкой Z(t)=, Z(t)= z_17j(t)+z_18j(t)+z_19j(t);

Итого Затраты Х’ (сумма строк 17+20) – (идентификатор VsegoResurs), он должен совпадать с 21 строкой.

Блок 2. Расчет коэффициентов Межотраслевого Баланса

Коэффициенты прямых затрат получены путем деления матрицы промежуточного потребления Аish на вектор-столбец валовых выпусков:

A=, где a_ij=_≥ 0, i=, j=.                                              (13)

Проверка на «продуктивность» выполняется путем суммирования коэффициентов прямых затрат. Получим вектор – строку А_PP, коэффициенты которой должны быть меньше единицы. Например, для 2013 года

%A_PP={0.4509  0.4825  0.5983  0.7330  0.6842  0.5786  0.3525    0.4029    0.4321    0.5306    0.2869    0.3127    0.2557  0.3055    0.3689}.

Матрица коэффициентов конечного использования:

Y= , где y_ij =≥ 0, i=, j=.                                              (14)

Матрица коэффициентов ВДС — получена путем деления матрицы Z (стоки 17-18 Баланса 2013 года Приморского края табл. 1) делим на вектор-столбец валовых выпусков (столбец 23):

Z=, где z_ij=≥ 0, i=, j=.                                                (15)

Коэффициенты полных затрат представлены матрицей В, B=(I—A)^-1.

Блок ресурсов модели (7)-(12) включает ограничения трудовые затраты.

Коэффициенты трудовых затрат:  t={, j=}                                   (16)

получены делением трудовых затрат по каждой отрасли на вектор-столбец валовых выпусков соответственно, например, для 2013 года: t =[1.7480  0.6778  0.8649  0.5903  0.4849  0.7445  1.1085   1.7390   0.5265  3.0534 0.7296  0.9269    2.7740  1.4984  2.5410], количество чел./1млн. продукции отрасли.

Блок мощностей включает ограничения по объемам произведенной продукции (отчет) за текущий (t^o) и плановый период (t^o+∆t):

X_i^ot(t^o) ≤ Х_i ≤ X_i^plan(t^o+∆t), i=,  X^plan(t^o+∆t)=X^ot(t^o)+10%X^ot(t^o)             (17)

где X^ot(t^o)={44050  47210  13870  193130  70120  80600  166890  14380  208930  4590  83600  78760  29920  440500  15350}′ — 23 графа табл. 4.

Эти данные используются для построения модели и последующих расчетов.

Блок 3. Построение коэффициентов инвестиций в  модели региона.

Инвестиции I(t)={I_v(t), v=}, вкладываемые в экономику региона по каждой отрасли, рассчитываются на основе данных о производственных фондах региона, полученных на стадии проектирования строительства.

Φ_о(t)={Φ_vo(t)=Φ_vp(t), v=, p∈ P_o}, ∀o∈O.                                (18)

где Φ_vo(t), o= —  вектор – столбец  объемов ОФ, который сформировал v-й вид деятельности в общем объеме ОФ o-й отрасли как суммы p∈P_o предприятий. Отсюда можем подсчитать общую сумму ОФ отрасли:

Φ_∑o(t)=Φ_vo(t), на ее основе, определить долю всех видов деятельности от величины суммы ОФ, которые в совокупности представляют вектор-столбец:

δ_о(t)={δ_vo(t)=Φ_vp(t)/Φ_∑o(t)}^T, o∈V_o,  где  =1, ∀o∈V_o,          (19)

В целом по всем видам деятельности {δ_vo(t), v=, o=}, представляет матрицу норм воспроизводства всех видов деятельности: V^δ=.

В нашем примере с численной моделью с пятнадцатью отраслями матрица V^δ=  построена исходя из предположения, что затраты на воспроизводственные фонды будут пропорциональны промежуточным затратам, представленных в матрице  A=. В итоге, после нормирования, матрица коэффициентов (норм) воспроизводства продукции по O=15 отраслям примет вид: V=,

Выполним проверку в системе Matlab: Vinv=[(V*0.1*Y)’; 0.1*Y ‘ ] .

В результате решения получим: Vinv=[1965  500  318  8964  586  3868  13093  120  15282  53  4396  5387  1359  1422;  1965  500  318  8964  586  3868  13093  120  15282  53  4396  5387  1359  1422], т.е. полученная сумма объемов продукции конечного спроса (конечного использования) за счет инвестиций по всем отраслям равна 0.1*Y и может использоваться в прогнозе на последующие периоды.

Объем инвестиций I_j, j= направлен на восстановление изношенных фондов и создания новых. Объем инвестиций I_j лежит в пределах от минимального восстановления изношенных основных фондов: I_j^min до величины инвестиций I_j^max= I_j^min +I_j^inv, выделенных фирмами, регионом и государством:

I_j^min ≤ I_j  ≤ I_j^max, j=, где I_j^min зависит от величины износа основных фонтов и определяется: I_j^min= KiznX^ot/KiFondov,  KiFondov – коэффициент использования основных фондов;

I_j^max= I_j^min +I_j^inv, I_j^inv= I_j^inv.f.+I_j^inv.reg.+I_j^inv.gos.: I_j^inv — величина инвестиций выделенных фирмами I_j^inv.f, регионом I_j^inv.reg, государством I_j^inv.gos. Объем выделенных инвестиций по каждой отрасли обозначим: I(t⁰+∆t)=[I₁, I₂, … , I₁₅].

Коэффициент «фондоотдачи» — равен отношению валового объема j-го вида продукции к объему  основных фондов KiFondov = X_j^val(t⁰)/Φ_j(t⁰), j=.

3.3. Построение численной динамической модели экономики  региона  

Математическая модель развития экономики региона представлена в виде векторной задачи (7)-(12). Используя рассчитанные коэффициенты, математическая модель экономики региона (7)-(12) преобразуется в численную модель.

Численная модель региональной экономики включает построение критериев (7)-(8) и ограничений (9)-(12).

Векторный критерий F(X, Ŷ, Ȳ) представлен множеством K=n+2 критериев. Он состоит из Y(t)={Ŷ +Ȳ} – n критериев максимизации конечного спроса  всех видов экономической деятельности (отраслей) региона, а также  критериев суммарного конечного спроса Y^val(t)= и валового выпуска регионального продукта X^val(t)= в (8). Ограничения представлены балансовыми уравнениями, ограничениями по трудовым ресурсам, производственным мощностям.

Балансовые уравнения задачи (9) включают три блока:

• матрицу IА=-(E—A), где E — единичная матрица, А={a_ij, i, j=}:

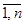• матрицу воспроизводства всех видов деятельности задачи V;
• матрицу конечного спроса E*Ȳ, размерностью 15*15, Ȳ(t)={ ȳ_j(t), j=}′ — вектор столбец конечного спроса 1*15.

Блок ресурсных затрат определяется только трудовыми ресурсами (11′), коэффициенты которых  t, j= рассчитаны в (16).

Производственные мощности определяются валовыми объемами производства (12):  X_i^ot(t^o) ≤ Х_i ≤ X_i^plan(t^o+∆t), i=, где X^ot(t^o) — 23 графа табл. 6.5; X^plan(t^o+∆t)=X^ot(t^o)+10%X^ot(t^o). % X^plan(t^o+∆t)=48460 51930 15260  212450 77130 88660 183570 15810 229820 5040 91960 86630 32910 48450 16880.

Объемы конечного использования 2013 по каждой отрасли представлены в 22 графе: Y(t)= Y_ot.

Y(t)={Ŷ +Ȳ}, Y_invOt ≤Ŷ≤Y_invMax, Y_bMin ≤Ȳ≤Y_bmax,

где Y_invOt=0.1*Y(t), Y_invMax=1.1*Y_invOt; Y_bMin,=0.9*Y_ot, Y_bMinY_bmax,=1.1*Y_bMin,

Ограничения по трудовым ресурсам региона определяются нижним пределом Tzmin = SummaTz = 985000, представленной в 22 строке баланса,  и верхнему пределу, который определяется увеличением  трудовых ресурсов на 5%, Tzmax=1.05*Tzmin=1034250.

В итоге, с учетом целенаправленности региона, представим практическую (численную) модель экономики региона (Приморского края) в виде векторной задачи линейного программирования во фрагментарном виде:

Opt F(X, Ŷ, Ȳ)={max Y(t⁰+∆t)=

{ max ŷ₁(t⁰+∆t) + ȳ₁(t⁰+∆t),…, max ŷ₁₅(t⁰+∆t) + ȳ₁₅(t⁰+∆t)},

max X ^val(t⁰+∆t)≡ x_j(t⁰+∆t), max Y^val(t⁰+∆t)≡ ȳ_j(t⁰+∆t)},                     (20)

-0.8537х₁+0.0738х₂+0.0310х₃+…+0.0354х₁₄+0.0153х₁₅ —     

                                       —0.0928ŷ₁-0.0501ŷ₂-…- 0.0224ŷ₁₄ -0.0034ŷ₁₅          — ȳ₁ ≤ 0;  (21)

0.0380х₁  -0.8180х₂+0.0002х₃+ …+0.0021х₁₄+0.0050х₁₅  —

—0.0028ŷ₁-0.0143ŷ₂— … — 0.0002ŷ₁₄-0.0001ŷ₁₅          — ȳ₂≤0;    (22)

 …

0.0221х₁+0.0187х₂+0.0310х₃+…-0.9709х₁₄+0.0254х₁₅   —     

—0.0065ŷ₁-0.0059ŷ₂-…-0.0086 ŷ₁₄-0.0026 ŷ₁₅        —ȳ₁₄≤0;     (34)

0.0011х₁+0.0069х₂+0.0210х₃+…+0.0142х₁₄-0.9669х₁₅ —

—0.0001ŷ₁-0.0009ŷ₂-…-0.0018ŷ₁₄-0.0014 ŷ₁₅      —ȳ₁₅≤0;    (35)

985000≤1.7480x₁+0. 6778x₂+…+1.4984x₁₄+2.5410x₁₅  0…0 ≤1034250,       (36)

44050≤x₁≤48460, 47210≤x₂≤51930,.., 440500≤x₁₄≤48450, 15350≤x₁₅≤16880,  (37)

1960≤ŷ₁≤ 2160, 500≤ŷ₂≤ 550, 320≤ŷ₃≤ 350,…,1420≤ŷ₁₄≤1560, 250≤ŷ₁₅≤270,  (38)

17680≤ȳ₁≤ 19450, 4500≤ȳ₂≤ 4950, …,1280≤ȳ₁₄≤14080, 2250≤ȳ₁₅≤2470,          (39)

X(t⁰+∆t)=KX*X(t⁰),  Ŷ(t⁰+∆t)=Kinv*Ŷ(t⁰),  Ȳ(t⁰+∆t)=KY* Ȳ(t⁰),

t⁰+∆t= t⁰, t⁰+1, …, t⁰+T,                                         (40)

где векторный критерий (20) F(X, Ŷ, Ȳ) включает 17 критериев: 15 – отраслевых и два системных, характеризующий регион в целом;

ограничения МОБ (21)-(35) содержат 15 неравенств, в которых вектор переменных X(t)={X(t)={x_j(t), j=}, Ŷ(t)={ŷ_j(t), j=}, Ȳ(t)={ȳ_j(t), j=}} имеет размерность равную 45;

ограничения МОБ (21)-(35) включает три блока: валовых объемов отраслей X(t), построенных на основе матрицы IА; блок конечного спроса Ŷ(t), полученный за счет инвестиций, построенных с помощью матрицы V, и блок объемов конечного спроса (использования) отраслей Ȳ(t), т. е. размерность матрицы МОБ 15*45; ограничения соответствуют (13);

неравенства (36) определяют два ограничения по трудовым ресурсам региона по нижнему и верхнему пределу, используя коэффициенты t_j^з, j=;

(37)-(40) — ограничения по мощностям  представляют X(t⁰)≤X(t)≤X(t⁰+∆t), X(t⁰) — отчетные данные за 2013 год, X(t⁰+∆t) – предполагаемые мощности; ограничения по конечному спросу с учетом инвестиций Ŷ(t⁰)≤Ŷ(t)≤Ŷ(t⁰+∆t)и без них Ȳ(t⁰)≤Ȳ(t)≤Ȳ(t⁰+∆t) на последующие на периоды (t⁰+∆t)∈T — на 2014 … и последующие годы;

(40) – равенства, которые определяют коэффициенты воспроизводства: по мощностям X(t⁰+∆t)=KX*X(t⁰), инвестициям  Ŷ(t⁰+∆t)=Kinv*Ŷ(t⁰) и конечному спросу Ȳ(t⁰+∆t)=KY*Ȳ(t⁰).Задача (20)-(40) решается в динамике с периодом планирования (∆t) правило, на один год ∆t=0, 1, 2, …, T.

Таким образом, модель экономики региона, представленная векторной задачи линейного программирования учитывает межотраслевой баланс, основные ограничения и динамику развития региона.

3.4. Методология моделирования и прогнозирования развития экономики региона

Процесс моделирования, в результате которого получим объемы валовых выпусков и конечное использование продукции отраслей региона включает в себя многократное решение векторной задачи линейного программирования (30)-(40). Для решения задачи (30)-(40) используется алгоритм, основанный на нормализации критериев и принципе гарантированного результата [25, 38], который представлен как последовательность шагов.

Шаг 0. Формирование исходных данных векторной задачи линейного программирования (20)-(40) в системе Matlab.

Формирование вектора критериев включает в себя исходные данные:

f = [0 0 …  0 0  -1  0 …  0   0  -1  0 … 0   0;           % max (ŷ₁ + ȳ₁)

0 0 …  0 0   0 -1 …   0   0   0 -1 … 0   0;           % max (ŷ₂ + ȳ₂)

…

0 0 …  0 0   0  0  … -1  0   0  0 … -1  0;           % max (ŷ₁₄ + ȳ₁₄)

0 0 …  0 0   0  0  …  0 -1   0  0 …  0 -1;           % max (ŷ₁₅ + ȳ₁₅)

-1 -1 … -1 -1  0  0 …  0  0    0  0 …  0  0;          % max X ^val

0  0  …  0  0  0  0 …  0  0  —1 -1 … -1 -1];         % max Y^val

Формирование ограничений: матрицы межотраслевого баланса и  трудовых ресурсов приобретают в системе Matlab следующий вид:

Вектор ограничений: b=[0 0 … 0 0 -Tzmin  Tzmax], где сумма трудовых затрат Tzmin=SummaTz=985000, Tzmax=1.1*Tzmin=1083500; Aeq=[]; beq=[];

ограничения на нижние и верхние валовые объемы регионального продукта, конечного спроса за счет инвестиций и конечного спроса по отраслям

X ={X^ot(t^o) ≤ Х ≤ X^plan(t^o+∆t), Y_invOt ≤Ŷ≤Y_invMax, Y_bMin ≤Ȳ≤Y_bmax}:

нижняя граница bl =[Xot YinvOt Yot]=[ Xot=44050 47210 13870…440500 15350 YinvOt =1960 500 320 …1420 250 Yot =17680 4500 2860 … 1280 2250];

верхняя граница ub=[Xbmax YinvMax Ybmax] =[ Xbmax =48460 51930 15260… 48450 16880 YinvMax= 2160 550 …270 19450 Ybmax=4950 3150…14080 2470].

Шаг 1. disp(‘Шаг 1. Решение по каждому критерию – наилучшее’)

Решение по первому критерию:

[x1,f1]=linprog(f(1,:),a,b,Aeq,beq,lb,ub)

где (…) – входные данные, представленные на шаге 0; [x1,f1] – выходные данные (результат решения), x1 — вектор оптимальных значений переменных по первому критерию, f1 – величина целевой функции в этой точке.

В результате решения по первому критерию получим:

x1=X₁^*= {X, Ŷ, Ȳ}, в т. ч. X=X1Max={x₁=46910 x₂=48780 x₃=14720 x₄=196430 x₅=72390 x₆=82630 x₇=16900 x₈=15420 x₉=211710  x₁₀=4920 x₁₁=8560 x₁₂=80530 x₁₃=31330  x₁₄=45680  x₁₅=16440}- валовые объемы отраслей;

Ŷ =I1Max={x₁₆=2160 x₁₇=530 x₁₈=340 x₁₉=9140 x₂₀=620 x₂₁=4030 x₂₂=13430 x₂₃=130 x₂₄=15570  x₂₅=50 x₂₆=4580 x₂₇=5610 x₂₈=1420  x₂₉=1480  x₃₀=260}- объемы конечного спроса отраслей за счет инвестиций;

Ȳ =Y1Max={x₃₁=19450 x₃₂=4680 x₃₃=2960 x₃₄=81050 x₃₅=5440 x₃₆=35180 x₃₇=118370 x₃₈=1110 x₃₉=138090  x₄₀=490 x₄₁=40030 x₄₂=48980 x₄₃=12620  x₄₄=13170  x₅₅=2320}- объемы конечного спроса отраслей;

f1=f₁^*= 21610 — объем продаж полученный первым подразделением от реализации X₁^*— объемов продукции. Объем продаж f₁^* = 21610 рассчитан из предположения, что первой отрасли отданы все глобальные ресурсы.

Аналогично получены результаты по остальным критериям: f_k , k=. Числовые значения результатов решения по критериям f_k^*, k= представлены на третьем шаге. Экономический смысл первого шага заключается в том, что каждой отрасли последовательно предоставляются все ресурсы и все мощности региона. Данные решения отображают значения конечного спроса, полученные путем вложения всех имеющихся средств у региона в развитие одной отрасли. В дальнейшем эти максимальные показатели развития каждой отрасли f_k^*, k= используем как цели развития этих отраслей при их совместной оптимизации.

Шаг 2. disp(‘Шаг 2. Решение по каждому критерию – наихудшее (антиоптимум) ‘)

Для этого каждый критерий умножается на минус единицу. Обращение к функции linprog(…) выглядит следующим образом:

[x1min,f1min]=linprog(-1* f (1,:),a,b,Aeq,beq,lb,ub)

В результате решения получили: x1min=X₁⁰={X,Ŷ,Ȳ} (верхний индекс «ноль»),

X=x1Min={x₁=45400 x₂=48720 x₃=14720 x₄=196260 x₅=72190 x₆=82440 x₇=168950 x₈=15440 x₉=211680  x₁₀=4940 x₁₁=85470 x₁₂=80420 x₁₃=31330  x₁₄=45630  x₁₅=16470};

Ŷ= I1Min={x₁₆=1960 x₁₇=530 x₁₈=340 x₁₉=9150 x₂₀=620 x₂₁=4030 x₂₂=13430 x₂₃=130 x₂₄=15560  x₂₅=50 x₂₆=4580 x₂₇=5600 x₂₈=1420  x₂₉=1480  x₃₀=270}

Ȳ=Y1Min={x₃₁=17680 x₃₂=4680 x₃₃=2960 x₃₄=81060 x₃₅=5430 x₃₆=35150 x₃₇=11835 x₃₈=1090 x₃₉=138010  x₄₀=490 x₄₁=39960 x₄₂=48940 x₄₃=12630  x₄₄=13180  x₅₅=2310};

f1min =f₁⁰= 19646 — объем продаж полученный первым подразделением от реализации X₁⁰— объемов продукции. Определяем  отклонение наилучшего и наихудшего решения d₁=f₁^*—f₁⁰, d1=-f1-f1min = 21610- 19646 = 1964.6.

Аналогично получены результаты по остальным критериям: d_k ={-f_k — fmin_k}, k=, K=17.

Шаг 3. Системный анализ результатов решения.

Для этого в точках оптимума x1=x₁^*, …, x17=x₁₇^* определим значение, как  критериев F={f_k(x_k^*(t)), k=} в натуральных единицах, так и в относительных в виде относительных оценок L={λ_k(x_k^*(t)), k=} по каждому критерию.

λ_k(x_k^*(t))=, k=, где f_k^*— наилучшее решение, полученное на первом шаге, и f_k⁰— наихудшее, полученное на втором шаге решения задачи.

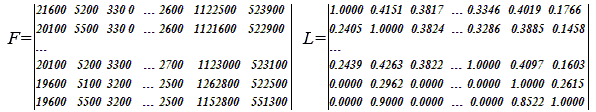
Шаг 4. Построение  λ – задачи — (Числовая модель экономики региона — Приморского края). Введем коэффициенты, определяющие развитие экономики региона: объемов валового регионального продукта KX=1; инвестиций Kinv=1; конечного спроса KY=1; Xmax = [KX*X  Kinv*Yinv  KY*Ymax] . Определим нижнюю и верхнюю границу переменных bl=Xmin; bu=Xmax.

В итоге λ – задача примет вид:

λ^o=max λ,                                                                                                 (41)

при ограничениях λ–((ŷ₁+ȳ₁)-f1min)/d1≤0,  λ–((ŷ₂+ȳ₂)-f2min)/d2≤0,  … ,        (42)

λ–((ŷ₁₆+ȳ₁₆)-f16min)/d16≤0, λ–((ŷ₁₇+ȳ₁₇)-f17min)/d17≤0,                (43)

и ограничениях (21)-(40),   t⁰+∆t= t⁰, t⁰+1, …, t⁰+T.                               (64)

Коэффициент λ – это максимальная относительная оценка или гарантированный уровень. λ показывает, до какого уровня подняты все критерии, измеренные в относительных единицах, т. е. λ^o ≤ λ_k (X^o(t)), k=.

Решение λ –задачи. Для решения  λ – задачи (41)-(64) в системе Matlab формируются исходные данные: критерий L (41); ограничения, представлены матрицей  A0 и вектором b0 (42)-(64):

b0=[-f1min/d1 —f2min/d2 …-f16min/d16  —f17min/d17  -Tzmin  Tzmax].

Формируется нижняя — Xmin и верхняя — Xmax границы на переменные:

Xmin = [Kmin*Xot     YinvOt                 0.9*Yot] ;            bl0 = [0.0 Xmin];

Xmax = [KX*Xbmax   Kinv*YinvMax   KY*0.95*Ybmax] ; bu0 = [1.0 Xmax].

Исходные данные (в Matlab) λ-задачи (41)-(64) используются:

• во-первых, для многократного прогнозирования (решения) на очередной (первый) год планирования путем изменения пределов вектора инвестиций (62) и выбора из полученных решений наиболее прие;
• во-вторых, для решении  динамике на  заданный период планирования (в нашем примере  три года,  ∆t=1, 2, 3, t⁰=2013 – этот год представлен отчетными данными Xmin) — результ такого прогнозирования представлен в следующем разделе этой главы (включая первый год).

Представленный метод, реализованный в виде программного обеспечения, и технология прогнозирования на одно — трех летний период представляет  «Методологию моделирования и прогнозирования развития экономики региона».

3.5. Прогноз и формирование основных  показателей  развития экономики региона на год

Прогноз и формирование показателей  развития экономики региона, в совокупности представляющие финансовый план региона, в т. ч. налоговые отчисления в доходную часть бюджета региона осуществляется путем многократного решения λ –задачи (41)-(64) в системе Matlab на планируемый период времени.

Решение λ –задачи (41)-(64) – планирование на 1 год.

В результате решения λ – задачи получили точку оптимума:

• X0 ={X0(1)=0.5259, X0(2:16)=1.0e+005* 0.4615 0.4961    0.1455    2.0324    0.7365    0.8443    1.7573    0.1507    2.2003    0.0481    0.8755    0.8238    0.3134    0.4618    0.1610, X0(17:31)=1.0e+004* 0.2161    0.0550    0.0349    0.8964    0.0644    0.4254    1.3093    0.0132    1.5282    0.0058    0.4836    0.5925    0.1495    0.1564    0.0275, X0(32:46)=1.0e+005* 0.1852    0.0471    0.0299    0.8539    0.0552    0.3646    1.2472    0.0113    1.4557    0.0050    0.4144    0.5077    0.1281    0.1341    0.0235}.
• L0 = 0.5259 – максимальный уровень, до которого подняты все критерии измеренные в относительных единицах, в этой точке.

Точка оптимума X0 показывает: X0(1)= L0= λ^o — максимальную относительную оценку,  X0(2:16) — валовой региональный продукт по каждой отрасли, X0(17:31)= YinvMax — конечный спрос, полученный за счет инвестиций, вложенных в экономику региона, и  X0(32:46)= YinvMax — конечное использование (спрос) , который представляет объем продукции соответствующей отрасли, полученный за счет основных фондов. Выполним проверку:

подсчитаем в точке X0 каждый критерий в натуральных единицах YinX0=[F(1,:)*X0(2:46) …  F(17,:)*X0(2:46)]. YinX0 =[ -20700   -5300   -3300   -94400   -6200   -40700   -137800   -1300   -160900   -600   -46300   -56700   -14300   -15000   -2600   -1150800   -546300];

соответствующие относительные оценки λ_k(X^o)=(f_k(X^o)- f_k⁰)/(f_k^*— f_k⁰), k= – в результате решения получили: λ_k(X^o)= [0.5259  0.5259  0.5259   … 0.5259  0.8224  0.8493];  в том числе доля прироста  за счет накопленных основных фондов составляет: λ_k(Ȳ^o)= [0 .4710  0 .4710  … 0 .4710], а доля прироста конечного спроса за счет инвестиций равна:

λ_k(Ŷ^o)= λ_k(X^o)-λ_k(Ȳ^o)=[0.0549  0.0549   … 0. 0549].

Результат говорит о том, что в оптимальной точке X^o темп роста каждой отрасли достигает не менее λ^o=0.5259 от своей установленной величины.

Используя полученные данные, рассчитаем основные экономические показатели развития региона на первый год планирования.

1) Оптимальные показатели (точка оптимума), которые включают:

Валовой объем производства (ресурсы); Конечный спрос, полученный за счет инвестиций; Конечный спрос, полученный за счет основных  фондов по всем отраслям на 1 год планирования — представлены в табл. 5.

Таблица 5 — Оптимальные показатели развития региона по всем отраслям

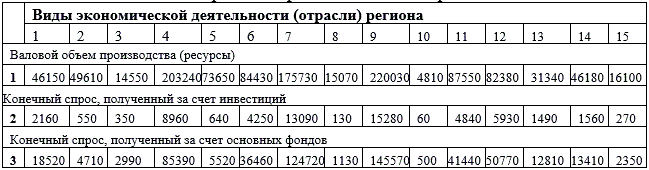
2) Суммарные показатели региона:

• суммарный валовой объем производства по региону (ресурсы), который лежит в пределах: sum(bl0(2:16))=1095400 ≤ sum(X0(2:16))=1150800 ≤ sum(bu0(2:16))=1205000;

• суммарный конечный спрос, полученный за счет инвестиций: sum(bl0(17:31))= 57600 ≤ sum(X0(17:31))= 59600 ≤ sum(bu0(17:31))= 62200;
• суммарный конечный спрос, полученный за счет  основных фондов: sum(bl0(32:46))= 518100  sum(X0(32:46))= 546300  sum(X0(32:46))= 569900$
• Общая сумма конечного спроса: sum(X0(17:31))+sum(X0(32:46))=605900.

3) Инвестиции в денежных единицах вкладываемые в каждую отрасль Inv2014= [X0(17:31)/KiFond]’=[5272  1342  853  21869  1571 10379  31941  323 37281 142  11797  14455  3646  3817  670], где iFond=SummaBal/SumOsnFond — коэффициент использования основных фондов, предполагая, что объем инвестиций полностью перейдет на стоимость основных фондов. При практических расчетах необходимы дополнительные исследования по оценке коэффициента использования основных фондов KiFond для каждой отрасли.

4) Затраты ресурсов при таком выпуске отраслей Rtrud=-A0(31,:)*X0= 1034250– количество человек необходимых для реализации взятых обязательств регионе; dr1=b0(31)-Rtrud= 42859 – отклонения ресурсов от планируемого роста; dr2=b0(32)-Rtrud  = 0, т. е.трудовые ресурсы региона используются полностью – они сдерживают дальнейший рост экономических показателей региона. (Аналогично можно рассчитывать и другие виды дефицитных ресурсов в регионе).

5) Темп роста каждой отрасли: в системе Matlab определяется вектором:

Rost_Vid = [-YinX0(1)/f1min; …- YinX0(15)/f15min] =[1.0526 … 1.0526]; аналогично вычисляется темп роста по экономике региона в целом: YinX0(16)/f16min= 1.0524 и темп роста по конечному спросу за счет основных фондов sum(YinX0(17))/f17min]=1.0529.

6) Заработная плата труда в регионе, рассчитывается, используя коэффициенты матрицы валовой добавленной стоимости Z табл.6.2:  Trud_Zp=[X0(2)*Zvds(1,1)  … X0(16)*Zvds(1,15)]  %Trud_Zp =[272.5 … 3780].

7) Налоговые отчисления по каждой отрасли: NalogX0 =[24660  21990 …30460  9640] (в т. ч. на федеральный, региональный и муниципальный уровни), — эти налоговые отчисления характеризуют налоговые поступления в доходную часть бюджета, являются началом для расчета бюджета региона;

8) Валовая прибыль экономики и валовой смешанный доход

Valsmeshdoh=[X0(2)*Zvds(3,1) …  X0(16)*Zvds(3,15)]= [405   …147].

9) Валовая добавленная стоимость (ВДС) по каждой отрасли ValDobStoim=[X0(2)*Zvds(4,1) …. X0(16)*Zvds(4,15)]= [25340 …  10160].  Сумма  валовых добавленных стоимостей отраслей региона определяет макроэкономический показатель – валовой региональный продукт (ВPП):

SumValDobStoim=sum(ValDobStoim) = 604580.

10) Промежуточное потребление по видам экономической деятельности Prom_Potrebl_VID=[A_PP.*X0(2:16)’] =[20810  23940 …. 14110  5940].

11) Финансовые потоки региона (Промежуточное потребление + Валовая добавленная стоимость):

FinansPotok=[Prom_Potrebl_VID+ValDobStoim]=[46150  49610  … 16100].

Суммарный финансовый поток регги она определяется следующим образом:

SummaFinansPotok =sum(FinansPotok) = 1150800.

Таким образом, представили основные экономические и макроэкономические показатели развития региона на годовой период.

Аналогично выполняются расчеты (прогноз) развития экономики региона 2-й и 3-й год на период планирования и оформляются в виде таблицы.

 Заключение

В целом результаты моделирования служат основой для различного вида финансовых задач и прежде всего для формирования бюджета региона.

Таким образом, математическая модель формирования развития региональной экономики дает возможность подсчитать основные экономические и макроэкономические показатели — валовые объемы и  оптимальный темп роста экономики региона с учетом: во-первых, межотраслевого баланса, во-вторых, инвестиций вкладываемых в каждую отрасль региона, в-третьих, с учетом ресурсных возможностей региона и его производственных мощностей. Построенная модель и результаты моделирования могут служить основой для разработки экономической политики региона, определяя линию поведения каждой отрасли (т.е. всех предприятий соответствующей отрасли) в совокупности. Авторы готовы участвовать в расчетах по прогнозированию развития других регионов.

Список литературы

1. Бюджетный кодекс Российской Федерации. – М.: ТК Велби, Изд-во Проспект, 2007. – 216 с.
2. Бакланов П. Я., Машков А. В. Пространственная дифференциация структуры экономики регионов арктической зоны россии// Экономика региона – 2015. — № 1. С.54-63.
3. Гранберг А.Г. Основы региональной экономики: учебник для вузов, — М: ГУ ВШЭ, 2004. 362 c.
4. Курнышев В.В. Региональная экономика. Основы теории и методы исследования: учебное пособие / В.В. Курнышев, В.Г. Глушкова. — 2-е изд., перераб. и доп. — М. : КНОРУС, 2011. — 272 с.
5. Машунин Ю. К. Региональная экономика и управление (Лекции, практика). Учебное пособие. — Владивосток: Изд-во ТГЭУ. 2009. – 348 с.
6. Машунин Ю. К., Машунин И. А. Моделирование развития и организация управления экономикой региона в рыночных условиях // Региональная экономика: теория и практика. 2010. № 7. С 2-9.
7. Машунин Ю.К. Теория управления. Математический аппарат управления экономикой. — М.: Логос, 2013. — 448 с.
8. Машунин Ю.К., Машунин И.А. Прогнозирование развития экономики региона с использованием таблиц «Затраты — Выпуск»// Экономика региона – 2014. — № 2. С.276-289.
9. Машунин Ю. К. Моделирование инвестиционных процессов в экономике региона. Монография.- LAMBERT Academic Publishing. 2014. 353p.
10. Машунин Ю.К., Машунин И.А. Моделирование и прогнозирование развитие экономики региона //Реструктуризация экономики: теория и инструментарий / под ред. Д-ра экон. Наук, проф. А.В. Бабкина. _ СПб. Изд-во Политехн. КН-та. 2015. С. 151-178.
11. Приморский край. Социально-экономические показатели: Статистический ежегодник. – Владивосток, Примрорскстат, 2014. 318 с.
12. Распоряжение от 14 февраля 2009 г. № 2001-р Правительства Российской Федерации о разработке базовых таблиц «затраты — выпуск» за 2011 год [Электронный ресурс] URL:http://www.gks/freedoc/new site/vvp/zatr-vip/zatr_vip.html
13. Региональная статистика: учебник/под ред. Е. В. Заровой, Г. И. Чудилина. – М.: Финансы и статистика, 2006. – 624 с.
14. Региональная экономика и пространственное развитие. В 2 т. Т. 1. Региональная экономика. Теория, модели и методы : учебник для бакалавриата и магистратуры / под общ. ред. Л. Э. Лимонова. — М. : Издательство Юрайт, 2014. — 397 с. — Серия : Бакалавр и магистр. Академический курс.
15. Регионы России. Социально-экономические показатели. 2014: Росстат. сб./ М., 2014, 900 с.
16. Таблицы «затраты-выпуск». – Режим доступа: URL:http://www.infostat.ru/ru/catalog.html.hfge=info&id=314
17. Татаркин А. И. Диалектика государственного и рыночного регулирования социально-экономического развития регионов и муниципалитетов // Экономика региона – 2014. — № 1. С.9-33.
18. Шумпетер Й. А. Теория экономического развития: капитализм, социализм и демократия // Предисл. В. С. Автономова; пер. с нем. В. С. Автономова, М. С. Любского, А. Ю. Чепуренко; пер. с англ. В. С. Автономова, Ю. В. Автономова, Л. А. Громовой, … —М.: Эксмо, 2007. — 864 с.
19. Leontyev, V. V., Input-output economics. New York, Oxford university press, 1966. – 436 p.
20. Tirole, Jean, 1993. The theory of Industrial Organization, The MIT Press. Cambridge, Massachusetts, London, England, 1993.- 695 p.

References

1. The budgetary code of the Russian Federation [Bjudzhetnyj kodeks Rossijskoj Federacii]. М. ТК Velbi, Publishing house the Prospectus, 2007. 216 p.
2. Baklanov P. Ja., Mashkov A. V. Spatial differentiation of structure of economy of regions of the Arctic zone of Russia [Prostranstvennaja differenciacija struktury jekonomiki regionov arkticheskoj zony Rossii]. region Economy 2015. No. 1. P. 54-63.
3. Granberg A. G. Of the Basis of regional economy [Osnovy regional’noj jekonomiki: uchebnik dlja vuzov]. М. GUVSHE, 2000. 495 p.
4. Kurnyshev V. V. Regional economy. Bases of the theory and methods of research. manual [Regional’naja jekonomika. Osnovy teorii i metody issledovanija. uchebnoe posobie]. 2nd prod., reslave. and additional M. KNORUS, 2011. 272 p.
5. Mashunin Ju. K. Regional Economics and management (lectures and practice) textbook [Regional’naja jekonomika i upravlenie (Lekcii, praktika). Uchebnoe posobie]. Vladivostok. Izd. TGEU, 2009. 348 p.
6. Mashunin Ju. K., Mashunin I. A. Simulation of the development and organization of management of regional economy in market conditions [Modelirovanie razvitija i organizacija upravlenija jekonomikoj regiona v rynochnyh uslovijah]. Regional Economics: theory and practice. 2010. № 7. P. 2-9.
7. Mashunin Ju.K. (2013). Control Theory. The mathematical apparatus of management of the economy [Teorija upravlenija. Matematicheskij apparat upravlenija jekonomikoj]. M. Logos. 448 p.
8. Mashunin Yu. K., Mashunin I. A. (2014). Prognozirovanie razvitiy economiki regiona c ispolzovaniev tablic Zatraty-vipusk [Prognozirovanie razvitija jekonomiki regiona s ispol’zovaniem tablic Zatraty — Vypusk]. Ekonomika regiona. 2, P. 276-289.
9. Mashunin Ju. K. Modeling of investment processes in region economy. Monograph [Modelirovanie investicionnyh processov v jekonomike regiona. Monografija]. LAMBERT Academic Publishing. 2014. 353p.
10. Mashunin Ju.K., Mashunin I.A. Modeling and forecasting development of economy of the region. Restructuring of economy the theory and tools [Modelirovanie i prognozirovanie razvitie jekonomiki regiona. Restrukturizacija jekonomiki teorija i instrumentarij]. SPb. Publishing house Politekhn. KN-that. 2015. Page 151-178.
11. Primorsky Krai. Socio-economic indicators. Statistical Yearbook [Primorskij kraj. Social’no-jekonomicheskie pokazateli. Statisticheskij ezhegodnik]. Vladivostok, Primorskstat, 2014. 318 p.
12. Order of February 14, 2009, N 201-R of the Government of the Russian Federation on the development of basic input — output table for 2011.[Rasporjazhenie ot 14 fevralja 2009 g. № 2001-r Pravitel’stva Rossijskoj Federacii o razrabotke bazovyh tablic zatraty — vypusk za 2011 god]. Mode of access: URL:http://www.gks/free doc/new site/vvp/zatr-vip/zatr_vip.html
13. Regional statistics. Textbook [Regional’naja statistika. Uchebnik]. pod red. E. V. Zarovoj, G. I. Chudilina M. Finance and statistics, 2006. 624 p.
14. Regional economy and spatial development. In 2 t. T. 1. Regional economy. Theory, models and methods. the textbook for a bachelor degree and a magistracy [Regional’naja jekonomika i prostranstvennoe razvitie. V 2 t. T. 1. Regional’naja jekonomika. Teorija, modeli i metody. uchebnik dlja bakalavriata i magistratury]. M. Publishing house of Yurayt, 2014. 397 p. a Series: Bachelor and master. Academic course.
15. Regions of Russia. Socio-economic indexes. 2014. Rosstat. Sb [Regiony Rossii. Social’no-jekonomicheskie pokazateli. 2014. Rosstat. sb]. M., 2014, 900 p.
16. The tables costs — output [Tablicy zatraty-vypusk]. Available from: URL:http://www.infostat.ru/ru/catalog.html.hfge=info&id=314
17. Tatarkin A. I. (2014). Dialectics of public and market regulation of a region and municipality socio-economic development [Dialektika gosudarstvennogo i rynochnogo regulirovanija social’no-jekonomicheskogo razvitija regionov i municipalitetov]. Economy of Region, 1, 9-33.
18. Shumpeter J. A. Theory of economic development, capitalism, socialism and democracy [Teorija jekonomicheskogo razvitija, kapitalizm, socializm i demokratija]. M. Eksmo, 2007.  864 p.
19. Leontyev, V. V., Input-output economics. New York, Oxford university press, 1966. 436 p.
20. Tirole, Jean, 1993. The theory of Industrial Organization, The MIT Press. Cambridge, Massachusetts, London, England, 1993. 695 p.

__________

[1] В 2003 году был проведен  анализ  статистических данных по РФ в системе национальных счетов в разрезе основных видов экономической деятельности. Результаты этого анализа были опубликованы в виде таблиц «Затраты — выпуск», где рассмотрена структура взаимосвязи агрегированных видов экономической деятельности {x_i(t)-y_i(t)}, i= (по строкам) по каждому виду экономической деятельности x_ij(t), j= (по столбцам) в процентном отношении  [16]. Данную структуру используем при построении модели межотраслевого баланса экономики Приморского края.