Краткосрочное прогнозирование величины валового регионального продукта на основе использования аппарата производственных функций
Short-term forecasting of the gross regional product based on the use of the apparatus of production functions
Авторы
Аннотация
В статье рассматриваются вопросы краткосрочного прогнозирования валового регионального продукта с использованием элементов модели Солоу. На примере экономики Ханты-Мансийского автономного округа были проведены оценки изменения значений указанного экономического показателя с горизонтом прогнозирования в один год. Для прогнозирования использовались производственные функции типа CES - функции и VES - функции. Результаты прогнозирования сопоставлялись с данными социально-экономической статистики Росстата РФ, представляемой в региональном разрезе.
Ключевые слова
Ханты-Мансийский автономный округ, региональная экономическая система, валовой региональный продукт, производственная функция, модель Солоу.
Финансирование
Работа выполнена при поддержке гранта РФФИ и Правительства ХМАО-Югра на реализацию научного проекта № 18-47-860016 «Компьютерное моделирование динамики социально-экономической системы ресурсодобывающего региона севера России c использованием теории роста, агентного подхода и ГИС-технологий».
Рекомендуемая ссылка
Краткосрочное прогнозирование величины валового регионального продукта на основе использования аппарата производственных функций// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №3 (63). Номер статьи: 6323. Дата публикации: 16.09.2020. Режим доступа: https://eee-region.ru/article/6323/
Authors
Abstract
The article discusses the issues of short-term forecasting of gross regional product using the elements of the Solow model. On the example of the economy of the Khanty-Mansiysk Autonomous Okrug, estimates were made of changes in the values of the specified economic indicator with a forecast horizon of one year. For forecasting, production functions of the type CES - functions and VES - functions were used. The forecasting results were compared with the data of socio-economic statistics of the Federal State Statistics Service of the Russian Federation, presented in a regional context.
Keywords
Khanty-Mansi Autonomous Okrug, regional economic system, the gross regional product, production function, Solow’s model.
Project finance
This work was supported by a grant from the Russian Foundation for Basic Research and the Government of the Khanty-Mansi Autonomous Okrug-Yugra for the implementation of the scientific project No. 18-47-860016 "Computer modeling of the dynamics of the socio-economic system of the resource-extracting region of the north of Russia using the growth theory, agent-based approach and GIS technologies."
Suggested Citation
Short-term forecasting of the gross regional product based on the use of the apparatus of production functions// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №3 (63). Art. #6323. Date issued: 16.09.2020. Available at: https://eee-region.ru/article/6323/
Введение
Для моделирования функционирования региональной экономической системы (РЭС), выработки управленческих решений в данной области и оценки результатов их реализации разработан целый ряд математических моделей различной сложности, которые можно объединить в следующие группы [1]:
- модели равновесия экономики – модели межотраслевого баланса, модели спроса и предложения;
- статистические и эконометрические модели, в том числе и модели, разработанные с использованием аппарата теории производственных функций (ПФ);
- имитационные модели и модели системной динамики;
- модели, разработанные с использованием интеллектуальных технологий таких, как экспертные системы и нейронные сети.
К моделям системной динамики принято относить и неоклассическую модель экономического роста Р. Соллоу [2,3]. Данная модель рассматривает экономическую систему как совокупность взаимодействующих между собой подсистем/секторов. Наиболее простой, но при определенных допущениях в целом достаточно работоспособной, является односекторная модель Р. Солоу. Теоретическому исследованию и практическому применению данной модели посвящено много работ зарубежных и отечественных исследователей (см., например [4]). Основной акцент данных работ сделан на теоретическом обосновании и получении аналитических выражений оптимального управления моделируемой экономической системы с учетом определенного перечня ограничений, в той или иной мере отражающих реальные условия ее функционирования. Возможность получения этих выражений обусловлена использованием в модели Р. Солоу производственной функции Кобба-Дугласа (ПФ Кобба-Дугласа) для описания производства конечного продукта в моделируемой системе [4,5]. Однако, данная ПФ является частным случаем производственных функций типа CES -функция и VES-функция [6-9] и в полной мере отражает изменения условий функционирования рассматриваемой экономической системы. Наряду с решением задач управления достаточно актуально, по мнению авторов, является и решение задачи прогнозирования изменений значений валового регионального продукта (ВРП), являющегося ключевым экономическим показателем, характеризующим состоянии и развитие рассматриваемой экономической системы. В данной статье авторы рассматриваются вопросы краткосрочного прогнозирования ВРП при использовании основных зависимостей односекторной модели Р. Соллоу. В качестве объекта исследования была выбрана региональная экономика Ханты-Мансийского автономного округа – Югра.
Теоретическая аспекты краткосрочного прогнозирования величины валового регионального продукта
Модель Солоу описывает односекторную макроэкономическую модель экономического роста [2-4], которая рассматривает региональную экономику, как неструктурированное замкнутое единое целое, в котором производится только один универсальный (агрегированный) конечный продукт (ВРП, Y), который может и потребляться, и инвестироваться. Экспорт и импорт продуктов не учитывается. Наряду с этим предлагается принять следующие допущения. Функционирование региональной экономики мало меняется при краткосрочном горизонте прогнозирования (один год) и для ее описания можно использовать неоклассическими линейно-однородными двухфакторными производственными функциями Y= f(K,L). Лаг между инвестициями в основной капитал (In) и стоимостью основных производственных фондов региональной экономики (K) не учитывается. Коэффициент, характеризующий выбытие основных производственных фондов считается известным. Затраты фактора труда (L) в рассматриваемом интервале времени изменяются с постоянным темпом прироста.
Модель Р. Соллоу с дискретным временем характеризуется следующей системой уравнений [2 — 4]:
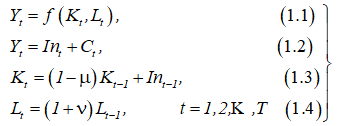(1)
Здесь ν – годовой темп прироста занятых в РЭС; μ – доля выбывших за год основных производственных фондов РЭС; t = 0 – базовый (начальный) год наблюдаемого периода времени функционирующей РЭС; t = T — конечный (последний) год этого же периода времени; K0, L0, In0 – известные значения этих переменных в базовый год наблюдаемого периода времени.
С формальной точки зрения выражение (1.2) является «инструментом» управления функционированием рассматриваемой региональной экономикой, т.к. Int в общем случае, принимая в качестве допущения наличие годового лага, оказывает влияние на стоимость основных производственных фондов в будущем году Kt+1, что, в свою очередь, влияет на соответствующую величину ВРП. Варьирование значений величины Int согласно (1.2) возможно за счет изменения величины потребления (фондов потребления) Сt. Однако на практике подобного рода действия затруднены по ряду причин. Так, например, администрация региона имеет крайне ограниченное влияние на изменения Int, т.к. подавляющее большинство предприятий его экономики являются частными и именно их владельцы, определяя инвестиционные программы развития этих предприятий, в конечно итоге и формируют величину Int. Формирование величины Сt связано с величиной валового регионального продукта опосредовано, т.к. в региональный фонд потребления включаются трансферты, дотации и субсидии различного рода. Таким образом, выражение (1.2) иллюстрирует экономическую сущность взаимосвязи между его компонентами, но его использование для оценок того изменения величины того ВРП сопряжено с определенными трудностями. Поэтому в данной работе указанное выражение не использовалось.
В выражении (1.1) применялись следующие типы ПФ:
- ПФ типа CES – функция (ПФ CES) [2,3]:
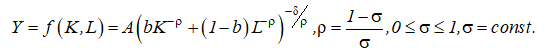(1)
- ПФ Кобба-Дугласа (ПФ КД) (частный случай ПФ типа CES – функция):
(2)
- ПФ типа VES-функция, методика построения которой описана в работе [8].
В выражениях (1,2) K, L – значения факторов затрат капитала и труда в экономической подсистеме рассматриваемой РЭС; α, β — эластичности конечного продукта Y по факторам затрат K, L; δ — показатель однородности ПФ: δ = 1; σ — эластичность замещения фактора затрат K фактором L; A – постоянная, значения которой, как и значения переменных α, β, σ, определяется методами математической статистики.
При идентификации указанных выше ПФ в качестве факторов затрат, как правило, используют следующие экономические показатели [9]:
- фактор затрат труда L – средняя численность занятых в региональной экономической подсистеме; затраты на оплату труда работников, занятых в экономике региона; фактически отработанное время в секторах экономики региона;
- фактор затрат капитала K — стоимость основных производственных фондов экономической подсистемы без учета или с учетом их загрузки, а также инвестиции в ее основной капитал.
При решении задач аналитического характера связанных, как отмечалось выше, с оценкой эффективности использования в региональной экономической системе ресурсов построение производственной функции допускает при соответствующем обосновании использование комбинаций всех перечисленных выше экономических показателей. Если же решаются задачи прогнозирования величины конечного продукта РЭС, то возможно использование только тех экономических показателей, для которых в настоящее время разработаны и апробированы модели оценки изменения их значений с учетом принятых горизонтов прогнозирования. В этом контексте из перечисленных выше показателей для L целесообразно использовать только показатель средней численности занятых в региональной экономической системе, а для K — стоимость ее основных производственных фондов.
Для оценки изменений значения фактора затрат труда L предлагается использовать следующее выражение [2,3]:
(3)
Здесь Lt.p, L0.ф — расчетное и фактическое значения средней численности занятых в региональной экономической системе в моменты времени t и t = 0 (для начального года рассматриваемого ретроспективного периода времени (t = [0,…,Т] функционирования РЭС) соответственно; ν – постоянная, определяемая методами математической статистики при анализе ретроспективных данных Lt.ф за этот же период времени.
Изменения значений фактора затрат капитала K за период t = [0,…,Т], в свою очередь, предлагается определять зависимостью [2,3]:
(4)
где Kt.p, Kt-1.ф — расчетная и фактическая стоимость основных производственных фондов региональной экономической системы в году t и t-1 соответственно; Int-1.ф — фактическая величина инвестиций в основные производственные фонды РЭС в году t-1; μt-1.ф — фактический коэффициент, характеризующий выбытие основных производственных фондов данной системы на конец года t-1.
Идентификацию ПФ осуществляют, представив Y, K и L в виде ряда базисных индексов относительно года Т0, рассматриваемого ретроспективного ряда исходных данных соответствующих экономических показателей. Если для величины ВРП Y и показателя численности занятых в региональной экономической системе формирование базисных индексов IY и IL не представляет особой сложности, то для определения значений базисных индексов физического объема стоимости основных производственных фондов экономической системы IK целесообразно использовать методику, предложенную в работе [10].
Краткосрочное прогнозирование величины ВРП предлагается осуществлять в результате выполнения следующей последовательности процедур:
- Для каждого
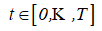по данным официальной социально-экономической статистики, представляемой в региональном разрезе, идентифицируются значения экономических показателей конечного продукта Yt.ф (ВРП), факторов затрат производства Kt.ф, Lt.ф и величины инвестиций в основной капитал Int.ф рассматриваемой региональной экономической системы. - Последовательности абсолютных значений Yt.ф, Kt.ф и Lt.ф преобразуются в ряды базисных индексов
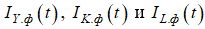. - Для временного интервала t = [0,…,Т] строятся двухфакторные неоклассические ПФ типа CES – функция (1), включая ПФ Кобба-Дугласа (2) [2-7,9], и типа VES – функция [8].
- Согласно (3,4) для t = Т+1 определяются расчетные значения KТ+1.p и LТ+1.p, которые преобразуются базисные индексы
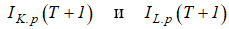сформированных ранее соответствующих рядов индексов (п.2). - С использованием построенных ПФ (п.3) рассчитывается значение индекса ВРП
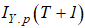на основании значений 
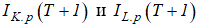. - Определяется относительная ошибка прогнозирования величины валового регионального продукта рассматриваемой экономической системы:
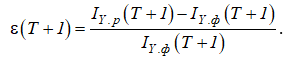(5)
Подготовка данных для моделирования функционирования РЭС ХМАО-Югра
Исходные статистические данные о социально-экономическом развитии РЭС ХМАО-Югра, публикуемые ежегодно Федеральной службой государственной статистики (Росстат) в статистическом сборнике «Регионы России Социально-экономические показатели» [11-13] и включающие значения ВРП (Yt.ф) и факторов затрат производства Kt.ф, Lt.ф, а также значения инвестиций в основной капитал Int.ф приведены в таблице 1.
Таблица 1. Статистические данные о функционировании РЭС ХМАО-Югра в период с 2001 г. по 2017 г.
| Год | ВРП в ценах текущего года Yt.ф, млн. руб. | Стоимость ОПФ на конец текущего года в текущих ценах Kt.ф, млн.руб. | Инвестиции в основной капитал в ценах текущего года Int.ф, млн. руб. | Средняя численность занятых в региональной экономике Lt.ф, тыс. чел. |
| 2001 | 538308,1 | 1300411 | 153 710,00 | 868,70 |
| 2002 | 589493,4 | 1765170 | 157 282,00 | 878,00 |
| 2003 | 760866,2 | 1969088 | 163 212,00 | 879,80 |
| 2004 | 956196,5 | 2203663 | 192 205,00 | 873,50 |
| 2005 | 1399335,9 | 2903606 | 223 318,00 | 877,10 |
| 2006 | 1594097,1 | 3346899 | 306 570,00 | 879,40 |
| 2007 | 1728340,2 | 4007371 | 381 342,00 | 880,60 |
| 2008 | 1937159,1 | 4852290 | 482 584,00 | 890,40 |
| 2009 | 1778637,1 | 5423503 | 472 195,00 | 897,40 |
| 2010 | 1971870,5 | 6382571 | 507 172,00 | 897,60 |
| 2011 | 2434202,0 | 6888515 | 636 976,00 | 903,60 |
| 2012 | 2703558,8 | 7953296 | 671 089,00 | 912,20 |
| 2013 | 2729122,4 | 8618035 | 718 871,00 | 916,10 |
| 2014 | 2860498,9 | 9546193 | 733867,00 | 917,20 |
| 2015 | 3154058,7 | 10275523 | 766070,00 | 1037,40 |
| 2016 | 3031163,3 | 11654167 | 799 253,00 | 1025,40 |
| 2017 | 3094817,7 | 12543037 | 942 184,00 | 1077,90 |
В таблице 2 приведены значения базисных индексов физического объема показателей Y, K и численности занятых в экономике РСЭС ХМАО-Югра L, которые использовались для идентификации производственных функций.
Таблица 2. Базисные индексы 
экономики РСЭС ХМАО-Югра за период с 2001 г. по 2017 г.
| Год | Индекс физического объема ВРП  |
Индекс физического объема основных производственных фондов  |
Индекс численности занятых в региональной экономике  |
| 2001 | 1,0000 | 1,0000 | 1,0000 |
| 2002 | 1,0250 | 1,0996 | 1,0107 |
| 2003 | 1,1193 | 1,1813 | 1,0128 |
| 2004 | 1,2077 | 1,2598 | 1,0055 |
| 2005 | 1,3575 | 1,3421 | 1,0097 |
| 2006 | 1,4484 | 1,4233 | 1,0123 |
| 2007 | 1,4948 | 1,5265 | 1,0137 |
| 2008 | 1,5381 | 1,6364 | 1,0250 |
| 2009 | 1,4643 | 1,7535 | 1,0330 |
| 2010 | 1,5082 | 1,8655 | 1,0333 |
| 2011 | 1,5218 | 1,9857 | 1,0402 |
| 2012 | 1,4929 | 2,1272 | 1,0501 |
| 2013 | 1,4944 | 2,2782 | 1,0546 |
| 2014 | 1,4944 | 2,4312 | 1,0558 |
| 2015 | 1,4788 | 2,5764 | 1,1942 |
| 2016 | 1,4788 | 2,7101 | 1,1804 |
| 2017 | 1,5098 | 2,8463 | 1,2408 |
Данные таблицы 2 в части значений базисного индекса средней численности занятых в региональной экономике показывают наличие скачкообразного роста данного показателя в интервале 2012 -2017 г. на фоне стагнации значения и достаточно равномерного устойчивого роста значения .
В таблице 3 приведены результаты построения моделей (3) изменения средней численности занятых в региональной экономической системе ХМАО- Югра при L0.ф = 868,7 тыс.чел. (таблица 1).
Таблица 3. Идентифицированные модели изменения средней численности занятых (3) в РЭС ХМАО- Югра
| № | Временной интервал | Идентифицированная зависимость (3) | R2 | Fрасч | Значимость критерия F |
| 1 | 2001 – 2012 г.г. |  |
0,955 | 215 | 1,373·10-7 |
| 2 | 2001 – 2013 г.г. |  |
0,963 | 283,5 | 1,146·10-8 |
| 3 | 2001 – 2014 г.г. |  |
0,887 | 390,4 | 6,089·10-10 |
| 4 | 2001 – 2015 г.г. |  |
0,722 | 33,72 | 8,386·10-5 |
| 5 | 2001 – 2016 г.г. |  |
0,753 | 42,63 | 1,912·10-5 |
В таблице 4 приведены значения коэффициентов выбытия (ликвидации) основных производственных фондов (в процентах) РЭС ХМАО- Югра на конец соответствующего года (таблица 2) [11-13].
Таблица 4. Коэффициенты выбытия основных производственных фондов РСЭС ХМАО-Югра
| Год/t | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| Коэффициент μt.ф | 0,6 | 0,7 | 0,7 | 0,8 | 0,8 | 0,65 |
Результаты прогнозирования значения валового регионального продукта экономической системы ХМАО- Югра
Идентификация производственных функций указанных выше ПФ и прогнозирование значений 
(п.2) осуществлялась в среде MatLab 15™. В таблице 5 представлены идентифицированные производственные функции Кобба-Дугласа (2) для каждого из рассматриваемых временных интервалов. Здесь же приведены значения коэффициента детерминации R2 для идентифицированных ПФ, соответствующие расчетные значения критерия Фишера Fр, а также табличные значения критерия Фишера FТ [14] для уровня значимости 0,05 и двух степеней свободы.
Таблица 5. Идентифицированные значения переменных ПФ типа Кобба-Дугласа для РЭС ХМАО-Югра
| Временной интервал, годы | Параметры ПФ Кобба-Дугласа | R2 | Fр/ FТ |
| 2001 – 2012 | А = 1,0541; α = 0,5802; β = 0,4198. | 0,7579 | 31,31/3,88 |
| 2001 – 2013 | А = 1,0748; α = 0,5023; β = 0,4977. | 0,6992 | 25,57/3,80 |
| 2001 – 2014 | А = 1,0923; α = 0,4460; β = 0,5540. | 0,6808 | 25,59/3,74 |
| 2001 – 2015 | А = 1,1133; α = 0,3755; β = 0,6245. | 0,5627 | 16,72/3,68 |
| 2001 -2016 | А = 1,1302; α = 0,3240; β = 0,6760. | 0,4880 | 13,37/3,63 |
В таблице 6, в свою очередь, представлены результаты построения производственных функции типа CES — функция (1) для тех же временных интервалов. Структура данной таблицы аналогична таблице 5, табличные значения критерия Фишера FТ приведены для уровня значимости 0,05 и трех степеней свободы [14].
Таблица 6. Идентифицированные значения переменных ПФ типа CES — функция для РЭС ХМАО-Югра
| Временной интервал, годы | Параметры ПФ типа CES — функция | R2 | Fр/ FТ |
| 2001 – 2012 | А = 1,0343; b = 0,89; σ = 0,1436. | 0,8657 | 64,46/3,49 |
| 2001 – 2013 | А = 1,0381; b = 0,9; σ = 0,1364. | 0,8560 | 65,36/3,41 |
| 2001 – 2014 | А = 1,0407; b = 0,91; σ = 0,1320. | 0,8497 | 67,81/3,34 |
| 2001 – 2015 | А = 1,0450; b = 0,9; σ = 0,1218. | 0,7468 | 46,33/3,29 |
| 2001 – 2016 | А = 1,0466; b = 0,88; σ = 0,1207. | 0,7855 | 51,27/3,24 |
Идентификация ПФ типа VES — функция согласно методике [8] позволяет сформировать только табличную форму представления данной функции для рассматриваемого временного интервала. Из-за ограничений объема данной работы авторы приводят только одну такую таблицу для интервала 2001 г.- 2016 г. (таблица 7).
Таблица 7. Результаты аппроксимации значений ВРП РЭС ХМАО-Югра ПФ типа VES – функция [8] для периода с 2001 г. по 2016 г.
| Год | IY.ф. | IY.р. | εt | σ |
| 2001 | 1,0000 | 0,9990 | 0,0011 | 0,0007 |
| 2002 | 1,0250 | 1,0983 | 0,0715 | 0,00071 |
| 2003 | 1,1193 | 1,1732 | 0,0482 | 0,0075 |
| 2004 | 1,2077 | 1,2385 | 0,0255 | 0,1483 |
| 2005 | 1,3575 | 1,3047 | 0,0389 | 0,1739 |
| 2006 | 1,4484 | 1,3661 | 0,0568 | 0,1971 |
| 2007 | 1,4948 | 1,4249 | 0,0468 | 0,0847 |
| 2008 | 1,5381 | 1,4408 | 0,0633 | 0,02951 |
| 2009 | 1,4643 | 1,4522 | 0,0082 | 0,02951 |
| 2010 | 1,5082 | 1,4527 | 0,0368 | 0,0041 |
| 2011 | 1,5218 | 1,4625 | 0,0390 | 0,00054 |
| 2012 | 1,4929 | 1,4766 | 0,0109 | 0,00004 |
| 2013 | 1,4944 | 1,4830 | 0,0076 | 0,00004 |
| 2014 | 1,4944 | 1,4848 | 0,0064 | 0,00004 |
| 2015 | 1,4788 | 1,6795 | 0,1357 | 0,00004 |
| 2016 | 1,4788 | 1,6597 | 0,1223 | 0,00004 |
Средняя относительная ошибка  |
0,0449 | |||
| Коэффициент R2 | 0,7871 | |||
Относительная ошибка εt между значениями IY.ф. и IY.р., рассчитанными при построении ПФ типа VES — функция определялась зависимостью структура которой, аналогична (5). Расчетные значения эластичности замещения факторов затрат производства σ для рассматриваемой РЭС показывают, что начиная с 2011 г. используемая ПФ типа VES-функция становится очень близкой к ПФ Леонтьева, для которой справедливо σ → 0. Это обусловлено тем, что начиная с указанного года рост величины ВРП практически прекратился при стабильном росте занятых в региональной экономике и росте стоимости ее основных производственных фондов (таблица 2).
В таблице 8 совместно приведены:
- статистические данные по ВРП IY.ф.(T+1) для соответствующего года, на который осуществляется прогнозирование ВРП (таблица 2);
- результаты прогнозирования значения ВРП с использованием ПФ Кобба-Дугласа, ПФ CES – функция (таблицы 4,5) и ПФ VES-функция (в том числе и таблица7).
Таблица 8. Прогнозные значения ВРП РЭС ХМАО-Югра на период с 2013 по 2017 г.г., полученные с использованием ПФ типа CES и VES функций
| Год прогнозирования | IY.ф.(T+1) | IY.р.(T+1), ПФ КД |
ε(T+1), ПФ КД |
IY.р.(T+1), ПФ CES |
ε(T+1), ПФ CES |
IY.р.(T+1), ПФ VES |
ε(T+1), ПФ VES |
| 2013 | 1,4943 | 1.7319 | 15,92 | 1,5696 | 5,04 | 1,5272 | 2,20 |
| 2014 | 1,4944 | 1,7213 | 15,19 | 1,5658 | 4,78 | 1,5286 | 2,29 |
| 2015 | 1,4788 | 1,6687 | 14,67 | 1,5563 | 5,24 | 1,5271 | 3,26 |
| 2016 | 1,4788 | 1,7112 | 15,71 | 1,5693 | 6,12 | 1,5565 | 5,25 |
| 2017 | 1,5098 | 1,7089 | 15,56 | 1,6150 | 9,12 | 1,5860 | 7,24 |
Расчетные значения величины ε(T+1) для всех использованных ПФ демонстрируют устойчивый рост. Это обусловлено тем, что начиная с 2012 г. в рассматриваемой экономической системе на фоне роста фондовооруженности труда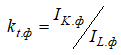 
рост величины средней производительности труда 
практически прекратился. Об этом также свидетельствую и значения IY.ф. и IL.ф. таблицы 2. Построение же неоклассических линейно-однородных ПФ предусматривает выполнение требования, связанного с их ростом (первая производная Y по факторам затрат K и L должна быть больше нуля), а также обеспечения выпуклости вверх этой функции (вторая производная Y по K и L должна быть меньше нуля). Вследствие этого построение ПФ на данных IY.ф., которые характеризуются достаточно устойчивым понижательным трендом (2011 – 2016 г.г.) приводит к росту расхождения между расчетными IY.р. и исходными IY.ф. данными.
В настоящее время администрации регионов РФ разрабатывают собственные прогнозы их социально-экономического развития, включающие и оценки значений ВРП. Горизонт прогнозирования достаточно широк, начиная от краткосрочного (до 3-х лет) до долгосрочного, например, «Программа 2020». Прогнозные значения ВРП РЭС ХМАО-Югра представлены его цепными индексами физического объема для оптимистического и пессимистического вариантов ее развития приведены на сайте правительства округа https://admhmao.ru/dokumenty/proekty-pravitelstva/. В таблице 9 для периода с 2013 г. по 2017 г. совместно представлены значения следующих показателей РЭС ХМАО-Югра:
- базисные индексы физического объема ВРП для прогнозов оптимистического
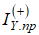и пессимистического 
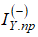вариантов развития экономики региона; - статистические данные о величине ВРП IY.ф.(T+1) (таблица 2);
- относительные ошибк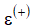и
и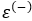 
, рассчитанные согласно (5), где в качестве IY.р.(T+1) выступают 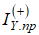и 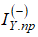соответственно.
Таблица 9. Прогнозные значения ВРП РЭС ХМАО-Югра по данным администрации округа на период с 2013 г. по 2017 г.
| Год прогнозирования | IY.ф.(T+1) | |
|
|
|
| 2013 | 1,4943 | 1,5093 | 0,0009 | 1,5033 | 0,006 |
| 2014 | 1,4944 | 1,4958 | 0,001 | 1,4824 | -0,008 |
| 2015 | 1,4788 | 1,4943 | -0,01 | 1,4869 | 0,005 |
| 2016 | 1,4788 | 1,4788 | 0 | 1,4714 | -0,005 |
| 2017 | 1,5098 | 1,4819 | 0,002 | 1,4723 | -0,004 |
Заключение и выводы
Анализ величин ε(T+1) (таблица 8) позволяет сделать вывод о том, что лучшее приближение расчетных значений ВРП РЭС ХМАО-Югра к его значениям, представленным в материалах Федеральной службой государственной статистики (Росстат), дает производственная функция типа VES функций. Вместе с тем, сопоставление ε(T+1) ПФ типа VES функция с величинами и (таблица 9) говорит о том, что специалисты администрации округа располагают для решения подобного рода задач более сложным и точным инструментарием. Наряду с этим, можно констатировать, что использование аппарата производственных функций для прогнозирования величины ВРП целесообразно в тех случаях, когда функционирование соответствующей региональной экономики характеризуется устойчивым ростом значений указанного экономического показателя при положительной динамике значений факторов ее затрат. Это, в свою очередь, допускает рассмотрение получаемых на основе производственной функции типа VES функций прогнозных значений ВРП, как его, своего рода, верхнюю оценку.
Литература
- Атаева А.Г., Исламова Д.В., Мустафин Э.Р., Орешников В.В. Сравнительный анализ моделей регионального развития// Управление экономическими системами: электронный научный журнал. 2011. № 34. – С. 55.
- Солоу Р.А. Перспективы теории роста //Мировая экономика и международные отношения. 1966. №8. – С. 69 – 77.
- Колемаев В.А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем. – М.: ЮНИТИ-ДАНА, 2005. – 295 с.
- Демин Н.С., Кулешова Е.В. Управление односекторной экономикой на конечном интервале времени в модели Солоу // Вестник Томского государственного университета. 2004. № 2 (84). – С. 52-56.
- Кокоткина Т.Н., Садовин Н.С., Царегородцев Е.И. Математические модели в прогнозировании развития экономики региона: монография. — Йошкар-Ола: Изд. ООО «СТИНГ», 2017. – 177 С.
- Клейнер Г. Б. Производственные функции: Теория, методы, применение / Г. Б. Клейнер – М.: Книга по Требованию, 2012. – 240 С.
- Экономико-математическое моделирование: учебник для студентов вузов/ Под общ. ред. И.Н. Дрогобыцкого. – М.: Издательство «Экзамен», 2004. – 800 C.
- Вольных Е.В., Кутышкин А.В., Никоноров Ю.Г.Построение d — однородной производственной VES – функции // Сибирский журнал индустриальной математики. – 2007. – Т. Х, № 2 (30). – С. 31–44.
- Сокол Г.А., Кутышкин А.В., Петров А.А. Об использование производственных функций для моделирования функционирования региональной экономики// Вестник Южно-Уральского государственного университета. Серия: Компьютерные технологии, управление, радиоэлектроника. 2017. Т. 17. № 4. С. 85-97.
- Бессонов В.А., Воскобойников И.Б. Динамика основных фондов и инвестиций в российской переходной экономике / В. Бессонов, И. Воскобойников. − Москва: ИЭПП, 2006. – 65 С.
- Статистический ежегодник (1990-2013): статистический сборник 25014.2: в 4 частях / Территориальный орган Федеральной службы государственной статистики по Тюменской области . – Официально издание. — Тюмень: [б. и.], 2014. Ч. 2(2) : Ханты-Мансийский автономный округ – Югра. – 452 С.
- Регионы России Социально-экономические показатели 2015// Статистический сборник. – М.: Федеральная служба государственной статистики (Росстат), 2015. – 1266 С.
- Регионы России Социально-экономические показатели 2018// Статистический сборник. – М.: Федеральная служба государственной статистики (Росстат), 2018. – 1162 С.
- Справочник по прикладной статистике. В 2-х т. Т 1: пер. с англ./Под ред. Ллойда Э., Линдермана У., Айвазяна С.А., Тюрина Ю.Н. – М.: Финансы и статистика, 1989. – 510 С.
References
- Atayeva A.G., Islamova D.V., Mustafin E.R., Oreshnikov V.V. Comparative analysis of regional development models [Sravnitel’nyy analiz modeley regional’nogo razvitiya]// Management of economic systems: electronic scientific journal. 2011.No 34. — P. 55.
- Solou R.A. Prospects for growth theory [Perspektivy teorii rosta]// World Economy and International Relations. 1966. No. 8. — S. 69 — 77.
- Kolemayev V.A. Economic and mathematical modeling. Modeling of macroeconomic processes and systems [Ekonomiko-matematicheskoye modelirovaniye. Modelirovaniye makroekonomicheskikh protsessov i sistem]. — M .: UNITI-DANA, 2005 .— 295 p.
- Demin N.S., Kuleshova Ye.V. Management of one-sector economy on a finite time interval in the Solow model [Upravleniye odnosektornoy ekonomikoy na konechnom intervale vremeni v modeli Solou]// Bulletin of the Tomsk State University. 2004. No. 2 (84). — S. 52-56.
- Kokotkina T.N., Sadovin N.S., Tsaregorodtsev Ye.I. Mathematical models in forecasting the development of the region’s economy [Matematicheskiye modeli v prognozirovanii razvitiya ekonomiki regiona]: monograph. — Yoshkar-Ola: Ed. LLC «STING», 2017. — 177 p.
- Kleyner G. B. Production functions: theory, methods, application [Proizvodstvennyye funktsii: Teoriya, metody, primeneniye] — M .: Book on Demand, 2012. — 240 p.
- Economic and mathematical modeling: a textbook for university students [Ekonomiko-matematicheskoye modelirovaniye: uchebnik dlya studentov vuzov]/ Ed. ed. I.N. Drohobytsky. — M .: Publishing house «Exam», 2004. — 800 C.
- Vol’nykh Ye.V., Kutyshkin A.V., Nikonorov YU.G. Construction of — homogeneous production VES — functions [Postroyeniye — odnorodnoy proizvodstvennoy VES – funktsii]// Siberian Journal of Industrial Mathematics. — 2007. — T. X, No. 2 (30). — S. 31–44.
- Sokol G.A., Kutyshkin A.V., Petrov A.A. On the use of production functions for modeling the functioning of the regional economy [Ob ispol’zovaniye proizvodstvennykh funktsiy dlya modelirovaniya funktsionirovaniya regional’noy ekonomiki]// Bulletin of the South Ural State University. Series: Computer technology, control, electronics. 2017.Vol. 17.No. 4.P. 85-97.
- Bessonov V.A., Voskoboynikov I.B. Dynamics of fixed assets and investments in the Russian transitional economy [Dinamika osnovnykh fondov i investitsiy v rossiyskoy perekhodnoy ekonomike]. — Moscow: IET, 2006 .— 65 p.
- Statistical Yearbook (1990-2013): statistical collection 25014.2: in 4 parts [Statisticheskiy yezhegodnik (1990-2013): statisticheskiy sbornik 25014.2: v 4 chastyakh]/ Territorial body of the Federal State Statistics Service in the Tyumen region. — Officially published. — Tyumen: [b. and.], 2014. Part 2 (2): Khanty-Mansiysk Autonomous Okrug — Yugra. — 452 S.
- Regions of Russia Socio-economic indicators 2015 [Regiony Rossii Sotsial’no-ekonomicheskiye pokazateli 2015]// Statistical collection. — M .: Federal State Statistics Service (Rosstat), 2015 .— 1266 p.
- Regions of Russia Socio-economic indicators 2018 [Regiony Rossii Sotsial’no-ekonomicheskiye pokazateli 2018]// Statistical collection. — Moscow: Federal State Statistics Service (Rosstat), 2018 .— 1162 p.
- Handbook of Applied Statistics [Spravochnik po prikladnoy statistike]. In 2 volumes. T 1: trans. from English / Ed. Lloyd E., Linderman U., Ayvazyan S.A., Tyurin Yu.N. — M .: Finance and statistics, 1989 .— 510 p
Еще в рубриках
Ханты-Мансийский автономный округ — Югра
Региональная экономика