Главная страница » Публикации » №1 (65) » Моделирование динамики численности занятых в региональной экономике (на материалах Ямало-Ненецкого автономного округа)

Моделирование динамики численности занятых в региональной экономике (на материалах Ямало-Ненецкого автономного округа)

Modeling population dynamics of employees in the regional economy (On materials of Yamal-Nenets Autonomous District)

Ямало-Ненецкий автономный округ
Экономика народонаселения и экономика труда

Авторы

Кутышкин Андрей Валентинович
доктор технических наук, профессор
Россия, Югорский государственный университет
avk_200761@mail.ru

Аннотация

В работе рассматривается использование эконометрических моделей и моделей системной динамики для оценки изменения среднегодовой численности занятых в региональной экономике Ямало-Ненецкого автономного округа, являющегося одним из ключевых ресурсодобывающих регионов России. При использовании эконометрических методов указанный макроэкономический показатель оценивался как среднее между его расчетными оценками, полученными по комбинированной модели соответствующего временного ряда и модели регрессии по временным рядам макроэкономических показателей, оказывающих наибольшее влияние на численность занятых в рассматриваемой региональной экономики. В модели системной динамики осуществлена модификация способа оценки ее ключевых компонентов, которая учитывает специфику рассматриваемого региона в демографическом аспекте. Расчетные значения численности занятых сопоставлялись с соответствующими статистическими данными в региональном разрезе, публикуемыми службой государственной статистики.

Ключевые слова

региональная экономика, население региона, численность занятых, системная динамика, эконометрическая модель.

Финансирование

Работа выполнена при поддержке гранта РФФИ и Правительства ХМАО-Югра на реализацию научного проекта № 18-47-860016 «Компьютерное моделирование динамики социально-экономической системы ресурсодобывающего региона севера России c использованием теории роста, агентного подхода и ГИС-технологий».

Рекомендуемая ссылка

Кутышкин Андрей Валентинович

Моделирование динамики численности занятых в региональной экономике (на материалах Ямало-Ненецкого автономного округа)// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №1 (65). Номер статьи: 6523. Дата публикации: 23.03.2021. Режим доступа: https://eee-region.ru/article/6223/

DOI: 10.24412/1999-2645-2021-165-23

Authors

Kutyshkin Andrej Valentinovich
Doctor of Technical Sciences, Professor
Russia, Yugorsk State University
avk_200761@mail.ru

Abstract

The paper considers the use of econometric models and models of system dynamics to assess changes in the average annual number of people employed in the regional economy of the Yamalo-Nenets Autonomous District, which is one of the key resource-extracting regions of Russia. When using econometric methods, the specified macroeconomic indicator was estimated as the average between its estimated estimates obtained using the combined model of the corresponding time series and the regression model for the time series of macroeconomic indicators that have the greatest impact on the number of employees in the regional economy under consideration. In the system dynamics model, a modification of the method for assessing its key components is carried out, which takes into account the specifics of the region under consideration in the demographic aspect. The calculated values of the number of employed were compared with the corresponding statistical data in the regional context, published by the State Statistics Service.

Keywords

regional economy, population of the region, number of employed, system dynamics, econometric model.

Project finance

This work was supported by a grant from the Russian Foundation for Basic Research and the Government of Khanty-Mansi Autonomous District-Yugra for the implementation of scientific project No. 18-47-860016 "Computer modeling of the dynamics of the socio-economic system of a resource-extracting region in the north of Russia using growth theory, agent-based approach and GIS technologies."

Suggested Citation

Kutyshkin Andrej Valentinovich

Modeling population dynamics of employees in the regional economy (On materials of Yamal-Nenets Autonomous District)// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №1 (65). Art. #6523. Date issued: 23.03.2021. Available at: https://eee-region.ru/article/6223/ 

DOI: 10.24412/1999-2645-2021-165-23

Print Friendly, PDF & Email

Введение

Моделирование динамики среднегодовой численности занятых в региональной экономике (L) представляет собой достаточно актуальную задачу, т.к. данный макроэкономический показатель используется не только для оценки фактора затрат труда в рассматриваемой экономической системе, но и оказывает определяющее влияние на состояние рынка труда в регионе. Для решения данной задачи чаще всего используются балансовый метод [1,2], эконометрические методы построения моделей L, учитывающие влияние макроэкономических показателей, характеризующих функционирование региональной экономики [3,4], и методы системной динамики [5-8]. Использование балансового метода, несмотря на то, что методика его реализации давно апробирована и достаточно хорошо себя зарекомендовала, в настоящее время затруднено из-за того, что в открытой печати практически отсутствуют детализированные в региональном разрезе таблицы «Выпуск-Затраты». Построение эконометрических моделей L в значительной мере зависит от достоверности исходных статистических данных и корректности определения факторов, оказывающих наиболее существенное влияние на изменение данного показателя [3,4]. Проблемы применения методов (моделей) системной динамики обусловлены их недостаточной или не в полной мере обоснованной спецификацией, которая была бы согласована с действующей системой государственной статистики, фиксирующей определенный перечень статистических показателей. Работы по данной проблематике условно можно объединить в две группы. К первой группе относятся работы, связанные с использованием модификаций базового дифференциального уравнения Мальтуса [5,6] для моделирования динамики L [7,8]. Вторая группа объединяет работы [9-11], связанные с использованием модели Лотки-Вольтерра для анализа регионального рынка труда и прогнозированием его динамики, включая оценку изменения значений L. В настоящее время разработка моделей второй группы затруднена тем, что ряд статистических показателей, используемых в этих моделях, Федеральной службы государственной статистики (ФСГС) не публикуется. В данной работе рассматривается использование эконометрических моделей и модификации уравнения Мальтуса – уравнения Ферхюлста (Verhulst P.F.) [5,6] для оценки изменений величины L региональной экономике Ямало-Ненецкого автономного округа (ЯНАО), являющегося одним из ключевых ресурсодобывающих регионов России.

 

Методы и принципы исследования

При моделировании эконометрическими моделями динамики среднегодовой численности занятых в региональной экономике L(t) целесообразно учитывать влияние на данный показатель, как численности населения региона, так и влияние предшествующих значений самого показателя, что в совокупности можно рассматривать как влияние демографического фактора региона. Комплексное влияние данного фактора на величину L(t) предлагается характеризовать следующей зависимостью:

,                              (1)

где L1.р(t) , L2.р(t) – значения среднегодовой численности занятых в региональной экономике, рассчитанные с учетом влияния изменения численности населения региона и динамики её ретроспективных значений соответственно.

 

Величину L1.р(t) предлагается определять выражением:

,                                   (2)

где  — регрессионная зависимость между временными рядами ретроспективных значений показателей Lf(t) и Nf(t).

 

Для идентификации зависимости (2) в настоящее время используется несколько методов [12,13]. Одним из универсальных является метод отклонения от тренда временного ряда, согласно которому выражение (2) приобретает следующий вид:

.                     (3)

 

Здесь , — значения L(t) и N(t), рассчитанные по идентифицированным трендам соответствующих временных рядов; c , d — постоянные определяемые при построении следующей регрессионной зависимости:

                                         (4)

где  (5)

 

Значение L2.р(t) предлагается оценивать комбинированной моделью следующего вида [12,13]:

                                     (6)

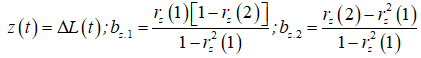
где rz(1), rz(2) – частные коэффициенты корреляции остатков z(t).

 

Корректность построенных регрессионных зависимостей (3,6) оценивалась c использованием общепринятых статистических критериев R2, критерия Фишера (F), критерия Дарбина-Уотсона (DW) [12].

Степень расхождения фактических Lf(t) и расчетных Lр(t) значений предлагается оценивать выражением:

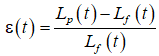.                                  (7)

 

Уравнение Ферхюльста П.Ф., с помощью которого можно описать динамику N(t) имеет вид [6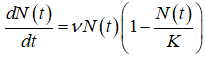-8]:

,                        (8)

где n — коэффициент, характеризующий динамику популяции (населения региона), которая была бы возможна при отсутствии ограничивающих факторов; K — максимально допустимая численность населения, которая может проживать в регионе.

 

Для оценки в первом приближении величины n предлагается использовать следующее выражение:

,                                     (9)

где ,  — коэффициенты, определяемые из модели Мальтуса [5,6] и характеризующие динамику численности населения региона и численности N1 экономически активного населения региона в трудоспособном возрасте.

Примем, что изменение между L(t) и N(t) существует взаимосвязь, которую в первом приближении, можно описать линейной зависимостью:

,                                    (10)

где a, b – определяются при построении регрессии по ретроспективным данным Lf(t) и Nf(t) на выбранном временном интервале.

 

После подстановки (8) в (10) получаем дифференциальное уравнение, характеризующее изменение L(t) для рассматриваемой региональной экономики [6]:

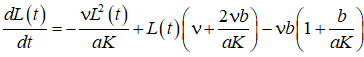.                    (11)

 

Актуальным является оценка величины K. В работах [7], [8], где объектом исследования была Рязанская область, был использован подход согласно которому выбирался регион (регион-эталон) с максимальной плотностью населения и близкими природно-климатическими условиями и исходя из соотношения площадей объекта исследования и выбранного региона-эталона рассчитывалось значение K. В результате реализации данного подхода расчетное значение K для указанного региона превысила 96 млн. чел. [7,8], что является более, чем оптимистической оценкой. По мнению автора для оценки K, особенно для таких регионов, как ЯНАО, использовать показатели роста численности их населения, которые рассчитывались при разработке планов освоения региональных природных ресурсов. Так для ЯНАО значение K предлагается принять равным 900 тыс. человек [14]. В качестве допущения примем, что в рядах Lf (t) и Nf (t) отсутствуют тренды. Близость фактических Lf (t) и расчетных L3.р(t) значений оценивается согласно (7).

Полученные результаты. Данные о среднегодовой численности занятых в региональной экономике Lf(t), численности населения Nf (t), численности экономически активного населения региона в трудоспособном возрасте N1.f (t) ЯНАО за период с 2001 г. по 2018 г. [15,16] приведены в таблице 1. Временные ряды Lf (t) и Nf (t) (таблица 1) характеризуются наличием следующих трендов:

.

Значения статистических критериев: R2 = 0,939; Fpасч = 34,84, табличное значение FT(0,05,2,15) = 3,633; расчетное значение DWpасч = 1,7286, табличное значение верхней границы DWup (2,18) = 1,239.

.

R2 = 0,928; Fpасч = 28,94, FT(0,05,2,15) = 3,633; DWpасч = 1,6786, DWup (2,18) = 1,239.

 

Таблица 1 – Значения Lf (t) (тыс. чел.), Nf (t) (тыс. чел.), N1.f (t) (тыс. чел.) для региональной экономики ЯНАО с 2001 г. по 2018 г.

Год Lf (t) Nf (t) N1.f (t) Год Lf (t) Nf (t) N1.f (t)
2001 319,00 503,10 302,35 2010 387,70 524,90 314,69
2002 330,90 508,60 305,46 2011 389,80 536,60 321,32
2003 353,00 510,80 306,71 2012 392,60 541,60 324,15
2004 357,30 514,60 308,86 2013 396,10 539,70 323,07
2005 359,70 517,40 310,44 2014 395,40 540,00 323,24
2006 355,90 521,60 312,82 2015 393,80 534,10 319,90
2007 357,20 524,00 314,18 2016 403,00 536,00 320,98
2008 364,60 523,00 313,61 2017 420,50 538,50 322,39
2009 368,50 524,10 314,24 2018 417,70 541,50 324,09

 

В свою очередь, выражения (3) и (6) имеют следующие характеристики:

(3): c = − 0,005, d = 0,376; R2 = 0,941; Fpасч = 36,111, FT(0,05,1,16) = 3,923; DWpасч = 1,689, DWup (1,18) = 1,118.

(6): bz.1 = 0,611, bz.2 = — 0,5621; R2 = 0,9533; Fpасч = 6,149, FT(0,05,2,15)  = 3,633; DWpасч = 2,327, DWup (2,18) = 1,239.

Сопоставление расчетных значений статистических критериев с соответствующими им табличными значениями можно сделать заключение о приемлемой корректности построенных моделей. В таблице 2 приведены значения Lf(t), расчетные значения L1.р(t) (3), L2.р(t) (6), Lр(t) (1) и ε(t) (7).

 

Таблица 2 – Расчетные значения Lр(t) для региональной экономики ЯНАО  с 2001 г. по 2018 г.

Год Lf(t),

(тыс. чел.)

 L1.р(t),

(тыс. чел.)

 L2.р(t),

(тыс. чел.)

 Lр(t),

(тыс. чел.)

 ε(t)
2001 319,0 328,733 321,426 325,079 -0,019
2002 330,9 335,671 329,196 332,434 -0,005
2003 353,0 341,294 344,121 342,707 0,029
2004 357,3 347,448 356,889 352,169 0,014
2005 359,7 353,153 352,870 353,011 0,019
2006 355,9 359,312 357,519 358,416 -0,007
2007 357,2 364,722 359,271 361,996 -0,013
2008 364,6 368,779 367,448 368,114 -0,010
2009 368,5 373,555 376,309 374,932 -0,017
2010 387,7 378,146 379,426 378,786 0,023
2011 389,8 386,769 393,684 390,227 -0,001
2012 392,6 392,796 388,715 390,756 0,005
2013 396,1 396,154 393,610 394,882 0,003
2014 395,4 400,267 398,362 399,315 -0,010
2015 393,8 401,973 399,978 400,976 -0,018
2016 403,0 406,545 403,228 404,887 -0,005
2017 420,5 411,270 413,408 412,339 0,019
2018 417,7 416,112 422,412 419,262 -0,004

 

На основании данных таблицы 1 коэффициенты a и b (10) имеют следующие значения: a = 2,13 , b = −747,067, а значения статистических коэффициентов равны: R2 = 0,872; Fpасч = 108,676, FТ (0,05;1,16) = 3,923; DWpасч = 1,246, DWup (1,18) = 1,118. Значения ,  определялись из зависимости, которая является решением уравнения Мальтуса [5,6]:

,                                  (12)

где в качестве ряда Y(t) выступали соответственно ряды Nf (t) и N1.f (t) (таблица 1).

 

Построенные для оценки  и  регрессионные зависимости, по своей структуре аналогичные (12), характеризуются следующими показателями:

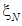  •  = 0,0041; R2 = 0,882; Fpасч = 76,278, FТ (0,05;1,16) = 3,923; DWpасч = 1,524, DWup (1,18) = 1,118.
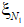  •  = 0,0187; R2 = 0,873; Fpасч = 74,563, FТ (0,05;1,16) = 3,923; DWpасч = 1,476, DWup (1,18) = 1,118.

Численное решение (11) L3.р(t) в среде MatLab2020ТМ при значениях переменных n = 0,0141; K = 900; a = 2,13; b = −747,067 приведено в таблице 3. В этой же таблице представлены значения относительной погрешности ε(t) (7) между Lf(t) и L3.р(t).

 

Таблица 3 – Расчетные значения L3.р(t) (тыс. чел.) и ε(t) по отношению к Lf(t) (тыс. чел.) для региональной экономики ЯНАО с 2001 г. по 2018 г.

Год Lf(t) L3.р(t) ε(t) Год Lf(t) L3.р(t) ε(t)
2001 319,00 325,14 0,013 2010 387,70 378,727 -0,0231
2002 330,90 335,901 0,0151 2011 389,80 384,451 -0,0137
2003 353,00 340,977 -0,0341 2012 392,60 390,261 -0,0060
2004 357,30 346,131 -0,0313 2013 396,10 396,159 0,0001
2005 359,70 351,362 -0,0232 2014 395,40 402,146 0,0171
2006 355,90 356,672 0,0022 2015 393,80 408,224 0,0366
2007 357,20 362,062 0,0136 2016 403,00 414,394 0,0283
2008 364,60 367,534 0,0080 2017 420,50 420,656 0,0004
2009 368,50 373,089 0,0125 2018 417,70 427,014 0,0223

  

Выводы

Значения ε(t), приведенные в таблицах 2 и 3, позволяют сделать следующие выводы. Относительная погрешность ε(t) между фактическими значениями среднегодовой численности занятых в региональной экономике ЯНАО и расчетными значениями данного показателя, полученными с использованием эконометрических моделей и модели системной динамики, не превышает 1,5%. Данное значение с учетом удовлетворительных соотношений между значениями стандартных статистических критериев и их предельно допустимыми табличными значениями при общепринятом уровне доверительной вероятности говорит о целесообразности использования указанных моделей для решения подобного рода задач. Наряду с этим следует отметить, что использование эконометрических моделей дает, как правило, заниженные оценки рассматриваемого макроэкономического показателя по отношению к его фактическим значениям, опубликованным в открытой печати структурами Федеральной службы государственной статистики. Использование же модели системной динамики, в свою очередь, дает в основном завышенную оценку данного показателя. Это, по мнению автора, объясняется тем, что построенные эконометрические модели учитывают демографический фактор региона, что нивелирует влияние экономических факторов, влияющих на численность занятых в региональной экономике. В модели системной динамики учет влияния экономических факторов опосредовано присутствует, что отражено в оценке скорости изменения населения региона, зависящей от динамики численности его трудоспособного населения. Например, снижение данного показателя на фоне роста общей численности населения обусловлено повышением спроса на местном рынке труда со стороны хозяйствующих субъектов.

 

Список литературы

  1. Ершов, Э. Б. Развитие и реализация идей модели межотраслевых взаимодействий для российской экономики // Экономический журнал ВШЭ. – 2008. – № 1. – С. 3 – 27.
  2. Зайцева ,И. В., Ворохобина, Я. В., Попова, М. В. Балансовая модель анализа и планирования трудового потенциала региона// Фундаментальные исследования. – 2014. – № 9. – С. 804 – 808.
  3. Косоруков, О. А., Петрикова, Е. М., Петрикова, С. М. Макроэкономические методы прогнозирования рынка труда в региональной экономике// Региональная экономика: теория и практика. – 2010. – № 45(180). – С. 10 – 25.
  4. Русина, А. Н., Карпычева, О. В. Моделирование сценарных условий прогнозирования кадровой потребности экономики региона // Экономика труда. – 2017. – № 4 (4). – С. 309 – 322.
  5. Pingle, M. Introduction dynamic analysis using Malthus’s Principle of Population// Economic Education. 2003. Vol. 34. №1, pp. 1-23.
  6. Базыкин, А. Д . Нелинейная динамика взаимодействующих популяций. — Москва-Ижевск: Институт компьютерных исследований, 2003. – 368 с.
  7. 7. Тихонов М.С. Построение прогноза доходной части бюджета Рязанской области на основе анализа односекторной макроэкономической модели региона // Известия РАЕН. Дифференциальные уравнения. – 2009. – № 14. – С. 132–141.
  8. Лазарева, И. А., Лискина, Е. Ю. Построение и идентификация односекторной модели экономики региона, учитывающей конечное потребление и конкуренцию за ограниченные ресурсы // Вестник РАЕН. –2016. – Т. 16. – № 3. – С. 36 – 40.
  9. Коровкин, А. Г. Динамика занятости и рынка труда: вопросы макроэкономического анализа и прогнозирования. – М.: МАКС Пресс, 2001. – 320 c.
  10. Мост, С.А. Прогноз динамики численности занятого населения на основе модели согласования спроса на рабочую силу и ее предложения// Вестник Самарского государственного экономического университета. – 2010. – №5(67). – С. 65-69.
  11. Хавинсон, М. Ю., Кулаков, М.П., Мищук, С. Н. Математическая модель динамики численности экономически активного населения и иностранной рабочей силы в регионе (на примере Еврейской автономной области) // Информатика и системы управления. – 2012. – № 1 (31). – С. 95–106.
  12. Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. — Т.2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ ДАНА, 2001. – 432 с.
  13. Временные ряды: анализ и прогнозирование: учеб. пособие / Н. В. Мамонова. – Иркутск : Изд-во БГУ, 2019. – 100 с.
  14. Стратегия развития Арктической зоны Российской Федерации и обеспечения национальной безопасности на период до 2020 года. [Электронный ресурс]. Режим доступа: http://www.arcticandnorth.ru/institut_arctic/strategy_AZRF_2010.pdf
  15. Статистический ежегодник: Стат. сб. Ямало-Ненецкий автономный округ в 2-х частях. Ч. I (I) (1990-2016)/ Управление Федеральной службы государственной статистики по Тюменской области, Ханты-Мансийскому автономному округу – Югре и Ямало-Ненецкому автономному округу. – Т., 2020. – 343 c.
  16. Статистический ежегодник: Стат. сб. Ямало-Ненецкий автономный округ в 2-х частях. Ч. II (2017-2019гг.)/ Управление Федеральной службы государственной статистики по Тюменской области, Ханты-Мансийскому автономному округу – Югре и Ямало-Ненецкому автономному округу. – Т., 2020. – 267c.

 

References

  1. Ershov, E. B. Development and implementation of ideas of the model of intersectoral interactions for the Russian economy [Razvitie i realizaciya idej modeli mezhotraslevyh vzaimodejstvij dlya rossijskoj ekonomiki]// HSE Economic Journal. – 2008. – No. 1. – P. 3 – 27.
  2. Zaitseva, I.V., Vorokhobina, Ya.V., Popova, M.V. Balance model of analysis and planning of the labor potential of the region [Balansovaya model’ analiza i planirovaniya trudovogo potenciala regiona]// Basic research. – 2014. – No. 9. – P. 804 – 808.
  3. Kosorukov, O. A., Petrikova, E. M., Petrikova, S. M. Macroeconomic methods of forecasting the labor market in the regional economy [Makroekonomicheskie metody prognozirovaniya rynka truda v regional’noj ekonomike]// Regional economy: theory and practice. – 2010. – No. 45(180). – P. 10 – 25.
  4. Rusina, A.N., Karpycheva, O.V. Modeling of scenario conditions for forecasting the personnel needs of the regional economy [Modelirovanie scenarnyh uslovij prognozirovaniya kadrovoj potrebnosti ekonomiki regiona]// Labor economics. – 2017. – No. 4 (4). – P. 309 – 322.
  5. Pingle, M. Introduction dynamic analysis using Malthus’s Principle of Population// Economic Education. – 2003. – Volume 34. – No. 1, – P. 1 – 23.
  6. Bazykin A.D. Nelinejnaya dinamika vzaimodejstvuyushchih populyacij [Nonlinear dynamics of interacting populations]. Moscow-Izhevsk, Institute of Computer Research, 2003. 368 p.
  7. Tikhonov, M.S. Forecasting the revenue side of the budget of the Ryazan region based on the analysis of a one-sector macroeconomic model of the region [Postroenie prognoza dohodnoj chasti byudzheta Ryazanskoj oblasti na osnove analiza odnosektornoj makroekonomicheskoj modeli regiona]// Izvestiya RANS. Differential Equations. – 2009. – No. 14. – P. 132 – 141.
  8. Lazareva, I.A., Liskina, E. Yu. Construction and identification of a one-sector model of the regional economy, taking into account final consumption and competition for limited resources [Postroenie i identifikaciya odnosektornoj modeli ekonomiki regiona, uchityvayushchej konechnoe potreblenie i konkurenciyu za ogranichennye resursy]// RANS Bulletin. – 2016. – Volume 16. – No. 3. – P. 36 – 40.
  9. Korovkin, A.G. Dinamika zanyatosti i rynka truda: voprosy makroekonomicheskogo analiza i prognozirovaniya [Dynamics of employment and labor market: issues of macroeconomic analysis and forecasting]. Moscow, MAKS Press, 2001. 320 p.
  10. Most, S.A. Forecast of the dynamics of the employed population based on the model of matching labor demand and supply [Prognoz dinamiki chislennosti zanyatogo naseleniya na osnove modeli soglasovaniya sprosa na rabochuyu silu i ee predlozheniya]// Bulletin of the Samara State Economic University. – 2010. – No. 5(67). – P. 65 – 69.
  11. Khavinson, M. Yu., Kulakov, M.P., Mishchuk, S. N. Mathematical model of the dynamics of the economically active population and foreign labor force in the region (on the example of the Jewish Autonomous Region) [Matematicheskaya model’ dinamiki chislennosti ekonomicheski aktivnogo naseleniya i inostrannoj rabochej sily v regione (na primere Evrejskoj avtonomnoj oblasti)]// Computer science and control systems. –- 2012. – No. 1(31). – P. 95 – 106.
  12. Ayvazyan, S.A. Prikladnaya statistika. Osnovy ekonometriki: Uchebnik dlya vuzov: V 2 t. 2-e izd., ispr. — T.2: Osnovy ekonometriki [Applied statistics. Fundamentals of econometrics: Textbook for universities: In 2 volumes, 2nd ed., Rev. — Vol.2: Fundamentals of Econometrics] Moscow, UNITY DANA, 2001. 432 p.
  13. Mamonova, N.V. Vremennye ryady: analiz i prognozirovanie: ucheb. posobie. [Time series: analysis and forecasting: Textbook for universities]. Irkutsk: BSU Publishing House, 2019. 100 p.
  14. Strategy for the development of the Arctic zone of the Russian Federation and ensuring national security for the period up to 2020. [Electronic resource]. Access mode: http://www.arcticandnorth.ru/institut_arctic/strategy_AZRF_2010.pdf
  15. Statistical Yearbook: statistical collection Yamalo-Nenets Autonomous Okrug in 2 parts. Part I (I) (1990 – 2016) [Statisticheskiy yezhegodnik (1990-2016): statisticheskiy sbornik 25023: v 2 chastyakh. Ch. I (I)]/ Territorial body of the Federal State Statistics Service in the Tyumen region, Khanty-Mansi Autonomous Okrug — Yugra and Yamalo-Nenets Autonomous Okrug. – Tyumen, 2020. – 343 p.
  16. Statistical Yearbook: statistical collection Yamalo-Nenets Autonomous Okrug in 2 parts. Part II (2017 – 2019) [Statisticheskiy yezhegodnik (1990-2016): statisticheskiy sbornik 25023: v 2 chastyakh. Ch. I (I)]/ Territorial body of the Federal State Statistics Service in the Tyumen region, Khanty-Mansi Autonomous Okrug — Yugra and Yamalo-Nenets Autonomous Okrug. – Tyumen, 2020. – 267 p.

Еще в рубриках

Ямало-Ненецкий автономный округ

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *