Политика полупроводниковой промышленности Китая, эффективность отрасли и синергетическое агрегирование на основе анализа методом GARCH
China semiconductor industry policy, industry efficiency and synergic aggregation based on GARCH analysis
Авторы
генеральный агент Japan Technomate Corporation в Китае слушатель программы "Доктор делового администрирования - DBA"
Аннотация
В статье представлено описание тенденция развития полупроводниковой промышленности Китая, делается вывод о необходимости оценки эффективности отрасли. Показано, что с помощью оценок дисперсии, основанных на экстремальных значениях, можно построить модели условной дисперсии с лучшими прогностическими свойствами, чем в случае моделей, основанных исключительно на доходности активов. Теоретические свойства оценок, основанных на экстремальных значениях, позволяют предположить, что их использование обеспечит получение более точных оценок волатильности. В статье представлено рассмотрение моделей класса GARCH, которые являются не только наиболее широко используемым, но и наиболее гибким инструментом моделирования и прогнозирования условной дисперсии.
Ключевые слова
модели класса GARCH, доходности акций, дисперсия, промышленность.
Рекомендуемая ссылка
Политика полупроводниковой промышленности Китая, эффективность отрасли и синергетическое агрегирование на основе анализа методом GARCH// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №2 (78). Номер статьи: 7815. Дата публикации: 03.06.2024. Режим доступа: https://eee-region.ru/article/7815/
DOI: 10.24412/1999-2645-2024-278-15
Authors
listener of the program "Doctor of Business Administration - DBA"
Abstract
The article presents a description of the development trend of the semiconductor industry, on the basis of which it is concluded that it is necessary to assess the efficiency of the industry. It is shown that with the help of estimates of variance based on extreme values, it is possible to construct conditional variance models with better predictive properties than in the case of models based solely on asset returns. The theoretical properties of extreme value estimates suggest that their use in conditional variance models will provide more accurate estimates of volatility. The article presents a review of GARCH class models, which are not only the most widely used, but also the most flexible tool for modeling and forecasting conditional variance.
Keywords
GARCH class models, stock returns, variance, industry
Suggested Citation
China semiconductor industry policy, industry efficiency and synergic aggregation based on GARCH analysis// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №2 (78). Art. #7815. Date issued: 03.06.2024. Available at: https://eee-region.ru/article/7815/
DOI: 10.24412/1999-2645-2024-278-15
Введение
В настоящее время ось разделения мирового рынка полупроводников проходит между США и Восточной Азией. Этот рынок можно разделить на три сегмента: 1) проектирование, 2) производство и 3) сборка, тестирование и упаковка полупроводников [1]. Проектирование — это прерогатива США, на долю которых приходится 65 % мирового рынка (15 % КНР, 17 % Тайваня). С точки зрения производства Тайвань доминирует на двух уровнях. Во-первых, он занимает 60% мирового рынка (по сравнению с 19% Южной Кореи, 8% США и 6% КНР). Во-вторых, он производит 92% самых передовых полупроводников (остальные 8% приходится на Южную Корею). К передовым полупроводникам относятся высокопроизводительные полупроводники размером несколько нанометров, позволяющие проводить высокопроизводительные вычисления, усиливающие возможности искусственного интеллекта и машинного обучения, которые используются для проектирования и производства энергоэффективных и мощных процессоров.
Проектирование, сборка и упаковка также являются специализацией Тайваня (53% мирового рынка), хотя Китаю удалось укрепить свои позиции в последние годы (19%). При этом основной целью промышленной политики Китая является технологическая самодостаточность. Это означает, например, возможность самостоятельного производства передовых полупроводников высокого класса. Несмотря на самые высокие в мире государственные расходы на эти цели (около 150 млрд долларов США в 2014-2020 гг.), Китай до сих пор не реализовал свое намерение [8].
В области полупроводников Китай остается асимметрично взаимозависимым от иностранных партнеров. Эту взаимозависимость необходимо учитывать как на технологическом, так и на коммерческом уровне. В технологической области Китай специализируется на производстве низкотехнологичных полупроводников — на его долю приходится 23% мирового производства полупроводников размером более 45 нм и 19% мирового производства полупроводников размером 28-45 нм. В области промежуточных полупроводников (10-22 нм) КНР производит всего 3% мировых поставок, а в части наиболее передовых технологий — менее 10 нм — полностью зависят от тайваньской TSMC и корейской Samsung [3, 8].
Аналогичная ситуация в области машин и программного обеспечения для производства полупроводников, где Китай зависит от импортных передовых инструментов автоматизации электронного проектирования (EDA) и оборудования для литографии в глубоком ультрафиолете (EUV), разрабатываемых в США и Голландии. Эта динамика сильно влияет на торговлю, при этом полупроводники остаются основным источником дефицита торгового баланса Китая. Этот дефицит постоянно усугубляется с 2014 г. -переломного момента активизации усилий Китая по достижению технологической самодостаточности. Таким образом, зависимость КНР от иностранных полупроводников по-прежнему является ключевой проблемой развития [2].
Результаты исследований
На основании вышеизложенного актуализируется необходимость поиска механизмов, направленных на повышение эффективности деятельности компаний полупроводниковой промышленности Китая, одним из которых является периодический анализ уровня доходности акций различными методами. Наблюдаемая волатильность цен на финансовые активы обычно идентифицируется с дисперсией или стандартным отклонением, основанным на квадрате отклонений распределения нормы прибыли на этот актив. Однако анализ научной литературы по описательной статистике показывает, что дисперсия — не единственный показатель доходности финансовых активов. Одной из редко используемых, хотя и очень гибких, мер дисперсии эмпирических распределений является диапазон, определяемый как разница между самым высоким и самым низким, с точки зрения ценности, наблюдением из выборки. Во избежание чрезмерного влияния выбросов на размер показателя определяется межквартильный размах, представляющий собой разность между квартилями распределения, симметричными медиане [4].
Среди основных описательных статистических показателей наиболее распространенным является межквартильный размах, представляющий собой разницу между третьим и первым квартилем эмпирического распределения. Естественно, здесь возникает вопрос о существовании связи между размахом и дисперсией. Нет сомнения в том, что между обоими показателями должна быть качественная связь, поскольку они измеряют одну и ту же особенность эмпирических распределений — дисперсию. Гораздо интереснее ответ на вопрос, существует ли между ними количественная связь. Чтобы ответить на этот вопрос, необходимо сделать некоторые предположения о процессе, генерирующем данные [7].
Предположение о том, что дисперсия доходности активов является постоянным параметром, характеризующим распределение этих норм доходности, в последующие годы стало общепринятым в теории финансов и нашло отражение даже в такой математически продвинутой модели, как модель ценообразования опционов, предложенная Блэком и Шоулзом в 1973 году. Затем новаторская статья Роберта Энгла 1982 года пролила новый свет на измерение риска. В ней Энгл представил модель авторегрессионной условной гетероскедастичности (модель ARCH — AutoRegressive Conditional Heteroscedasticity) и дал начало новой ветви финансовой эконометрики, занимающейся моделированием изменяющейся во времени условной дисперсии доходности [6].
Развитие моделей условной дисперсии в последующие годы, вероятно, стало неожиданностью даже для самого автора модели ARCH, однако, несмотря на все более сложные функциональные формы этих моделей, подавляющее большинство из них основано на общем допущении относительно данных, которые используются: основным источником информации о волатильности доходностей являются временные ряды доходностей. С начала 21 века появились работы, в которых предлагались модели условной дисперсии с использованием альтернативных методов оценки волатильности, в частности, оценок дисперсии, основанных на экстремальных значениях. Основной мотивацией этого вида работ являлось желание оценивать модели с учетом большего объема информации. Классические модели условной дисперсии, оцениваемые по дневным данным или только на временных рядах доходностей, извлекают информацию только из дневных цен закрытия актива, при этом одинаково легко можно получить ряды цен открытия, минимальных и максимальных цен — эти данные используются во многих методах технического анализа и для подавляющего большинства активов широко доступны [5].
Пусть rt обозначает норму доходности, рассчитанную на основе стоимости портфеля акций yt в момент времени t по отношению к значению при (t − 1):
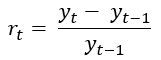 (1)
(1)
Согласно модели ARCH(p), значение нормы прибыли в момент времени t зависит от норм доходности в предыдущие моменты времени и значения случайной величины ε t:
![]() (2)
(2)
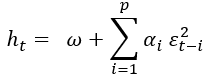 (3)
(3)
В классических спецификациях модели ARCH предполагается, что условное математическое ожидание μt равно нулю и, следовательно, опущено, а εt = rt.
Боллерслев предложил обобщить модель (2), введя модель GARCH(p,q), в которой он сделал условную дисперсию дополнительно зависимой от дисперсии в предыдущие временные моменты:
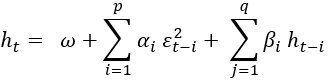 (4)
(4)
На практике наиболее часто используемой моделью является GARCH(1,1):
![]() (5)
(5)
Для ARCH(1) и GARCH(1,1) модель принимает следующий вид:
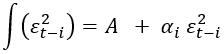 (6)
(6)
Константа A в модели ARCH(1) равна ω, а в модели GARCH(1,1) A = ω + β1ht−1 . Поскольку функция (6) представляет собой симметричную параболу вокруг нуля, она не позволяет моделировать динамику доходности.
Затем было проведено обобщение модели GARCH для моделирования, результат получил название модель AGARCH, где:
![]() (7)
(7)
В этом случае модель принимает следующий вид:
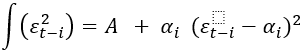 (8)
(8)
Как и в случае с моделью GARCH, это парабола, но в данном случае она достигает минимума для ![]() .
.
Тогда же было предложено еще одно обобщение модели GARCH, известное как GJR-GARCH, в отличие от более ранних моделей, график этой функции представляет собой не параболу, а складывание плеч двух разных парабол. Также была использована модель EGARCH, предложенная Нельсоном.
Для анализа использовались ставки доходности акций китайских компаний полупроводниковой промышленности, котируемых на Шанхайской фондовой биржи:
- LONGi Green Energy Technology Co., Ltd. производит и продает фотоэлектрические продукты и решения по всему миру — LONGI,
- NAURA Technology Group Co., Ltd. занимается исследованиями, разработками, производством и продажей электронного оборудования и компонентов в Китайской Народной Республике — NAURA,
- Hygon Information Technology Co., Ltd. занимается исследованиями и разработками продуктов и систем с вычислительными чипами — HYGON,
- для сравнения индекс Shanghai SSEC.
Доходность была рассчитана на основе цен закрытия. Для того, чтобы определить, в какой степени можно говорить о динамике эффективности предприятий на основе ряда норм доходности акций, были оценены следующие модели: GARCH, AGARCH, GRJ-GARCH, EGARCH и EGARCH со значением параметра, отвечающего за асимметрию NIF, эта модель позже получила обозначение rEGARCH. Были выбраны два показателя соответствия: логарифм из функции надежности LLF и информационный критерий AIC Akaike.
AIC = −2LLF + 2K (9)
Где K — количество параметров. Чем выше эффективность, тем ниже значение AIC.
Таблица 1 — Значения LLF для рассматриваемых моделей
| Модель | Количество параметров | LONGI | NAURA | HYGON | SSEC |
| GARCH | 4 | 6121,155 | 5720,325 | 6668,212 | 6695,879 |
| AGARCH | 5 | 6122,737 | 5720,735 | 6672,416 | 6726,48 |
| GJR-GARCH | 5 | 6122,727 | 5721,406 | 6672,736 | 6732,326 |
| EGARCH | 5 | 6120,124 | 5718,723 | 6670,814 | 6740,994 |
| rEGARCH | 4 | 6118,713 | 5718,082 | 6669,653 | 6688,081 |
Анализируя представленные в таблицах 1 и 2 значения показателей качества соответствия моделей, можно сделать вывод, что по всем показателям наилучшими оказались модели, учитывающие асимметрию функции информационного воздействия.
Таблица 2 — Значения AIC для соответствующих моделей
| Модель | Количество параметров | LONGI | NAURA | HYGON | SSEC |
| GARCH | 4 | -12223,302 | -11422,362 | -13316,432 | -13371,717 |
| AGARCH | 5 | -12224,462 | -11421,182 | -13322,832 | -13430,863 |
| GJR-GARCH | 5 | -12224,442 | -11422,522 | -13323,472 | -13442,544 |
| EGARCH | 5 | -12219,242 | -11417,162 | -13319,632 | -13459,866 |
| rEGARCH | 4 | -12218,422 | -11417,882 | -13319,312 | -13356,135 |
В случае акций компаний модели AGARCH и GJERCH-GARCH оказались лучшими, в то время как в случае SSEC EGARCH является лучшей моделью. Однако тот факт, что модели, учитывающие асимметрию, лучше подходят, не является достаточным основанием для того, чтобы сделать вывод о возникновении эффекта в ряду норм доходности акций. Еще необходимо проверить, достаточно ли велика разница. Формально необходимо было бы проверить гипотезу о нулевом значении параметра, отвечающего за асимметрию, в отдельных моделях.
![]() (10)
(10)
Для проверки этой гипотезы можно использовать тест, основанный на частном тесте отношения правдоподобия (LRT):
LRT = 2(LLF1 − LLF0) (11)
В случае, когда гипотеза верна, статистика LRT имеет асимптотическое χ-распределение (2p1− p0), где p1 и p0 обозначают номера параметров соответствующих моделей. Использование этого теста для сравнения двух моделей, одна из которых содержит параметр, отвечающий за моделирование эффективности, а другая нет, должно дать ответ на возникновение эффекта. Модели AGARCH и GJR-GARCH сравнивались с моделью GARCH, а модель EGARCH — с моделью rEGARCH.
Таблица 3. Статистические значения теста LRT
| Модель | LONGI | NAURA | HYGON | SSEC |
| AGARCH | 3,2635 | 0,9187 | 8,4043 | 61,1240 |
| GJR-GARCH | 3,1445 | 2,1630 | 9,0410 | 71,8084 |
| EGARCH | 3,8210 | 1,2750 | 2,4221 | 103,7112 |
Критическое значение для всех вычисляемых значений тестовой статистики одинаково χ (20,05,1) = 3,8415. Из трех компаний, только данные HYGON отвергают гипотезу об отсутствии асимметрии на уровне значимости 0,05. При этом стоит отметить, что даже в этом случае значения тестовой статистики для SSEC в разы выше.
Заключение
Проведенные анализы показали, что только в случае с доходностью акций компании HYGON можно говорить о повышении эффективности. Однако даже в этом случае динамика эффективности значительно меньше, чем в случае с индексом SSEC. Хотя из-за небольшого объема проведенных исследований не представляется возможным сделать слишком обширные выводы, полученные результаты свидетельствуют о том, что использование моделей может помочь понять уровень эффективности деятельности компаний на основе уровня доходности акций.
Список литературы
- Зеленский, А.А., Морозкин, М.С., Грибков, А.А. Обзор полупроводниковой промышленности в мире и России: производство и оборудование // Известия вузов. Электроника. 2021. №6. С.468-480.
- Ильина, С.А. Рынок полупроводников: глобальная цепочка создания стоимости и динамика в условиях кризиса // Вестник Института экономики Российской академии наук. 2022. №3. С. 112-125. doi: 10.52180/2073-6487_2022_3_112_125
- Седых, Н.В. Мировой рынок полупроводников: основные тенденции и проблемы // Вестник Академии знаний. 2023. №2 (55). С.222-224.
- Симонов, П.М., Ахуньянова, С.А. Сравнительный анализ методик ar-garch и p-адического прогнозирования волатильности финансового рынка // Вестник ПГУ. Серия: Экономика. 2019. №1. С.69-92.
- Трифонов, Ю.С., Потанин, Б.С. Многомерная асимметричная garch-модель с динамической корреляционной матрицей // Финансы: теория и практика. 2022. №2. С.204-218.
- Jane,, Ding, C G. On the multivariate EGARCH model. Applied Economics Letters. 2009;16(17):1757-1761. DOI: 10.1080/13504850701604383.
- Miralles-Marcelo,L., Miralles-Quiros, J.L., Miralles-Quiros, M. del M. Multivariate GARCH Models and risk minimizing portfolios: The importance of medium and small firms. The Spanish Review of Financial Economics. 2013;11(1):29-38. DOI: 10.1016/j.srfe.2013.03.001
Bibliography
- Zelenskiy, A.A., Morozkin, M.S., Gribkov, A.A. Overview of the Semiconductor Industry in the World and Russia: Production and Equipment. [Obzor poluprovodnikovoy promyshlennosti v mire i Rossii: proizvodstvo i oborudovanie]. // Izvestiya VUZov. 2021. No.6. P.468-480.
- Ilyina, S.A. Semiconductor Market: Global Value Chain and Dynamics in Crisis Conditions. [Rynok poluprovodnikov: globalnaya tsepochka sozdaniya stoimosti i dinamika v usloviyakh krizisa]. // Vestnik Instituta ekonomiki Rossiyskoy akademii nauk. No.3. P. 112-125. doi: 10.52180/2073-6487_2022_3_112_125
- Sedykh, N.V. Global Semiconductor Market: Key Trends and Issues. [Mirovoy rynok poluprovodnikov: osnovnye tendentsii i problemy]. // Vestnik Akademii znanii. No.2 (55). P.222-224.
- Simonov, P.M., Akhunyanova, S.A. Comparative Analysis of AR-GARCH and P-Adic Volatility Forecasting Methods in Financial Market. [Sravnitelnyy analiz metodik ar-garch i p-adicheskogo prognozirovaniya volatil’nosti finansovogo rynka]. // Vestnik PGU. Seriya: Ekonomika. 2019. No.1. P.69-92.
- Trifonov, Yu.S., Potanin, B.S. Multidimensional Asymmetric GARCH Model with Dynamic Correlation Matrix. [Mnogomernaya asimmetrichnaya garch-model’ s dinamicheskoy korrlyatsionnoy matritsey]. // Finansy: teoriya i praktika. No.2. P.204-218.
- Jane,, Ding, C G. On the multivariate EGARCH model. Applied Economics Letters. 2009;16(17):1757-1761. DOI: 10.1080/13504850701604383.
- Miralles-Marcelo,L., Miralles-Quiros, J.L., Miralles-Quiros, M. del M. Multivariate GARCH Models and risk minimizing portfolios: The importance of medium and small firms. The Spanish Review of Financial Economics. 2013;11(1):29-38. DOI: 10.1016/j.srfe.2013.03.001
Еще в рубриках
Китай
Мировая экономика