Главная страница » Публикации » №2 (82) » Метод восстановления данных по миграционной ситуации региона с использованием имитационного моделирования на основе агрегированных данных Росстата

Метод восстановления данных по миграционной ситуации региона с использованием имитационного моделирования на основе агрегированных данных Росстата

Method of data recovery on the migration situation of the region using simulation modeling based on Rosstat aggregated data

Регионы России
Региональная экономика

Авторы

Кораблев Юрий Александрович
к.э.н., научный сотрудник института цифровых технологий факультета информационных технологий и анализа больших данных
Российская Федерация, Финансовый университет при Правительстве Российской Федерации
YuAKorablev@fa.ru
Михайлова Светлана Сергеевна
д.э.н., ведущий научный сотрудник института цифровых технологий факультета информационных технологий и анализа больших данных
Российская Федерация, Финансовый университет при Правительстве Российской Федерации
SSMihajlova@fa.ru
Концевая Наталья Валерьевна
к.э.н., научный сотрудник института цифровых технологий факультета информационных технологий и анализа больших данных
Российская Федерация, Финансовый университет при Правительстве Российской Федерации
NVKontsevaya@fa.ru
Будаев Евгений Сергеевич
к.т.н., научный сотрудник института цифровых технологий факультета информационных технологий и анализа больших данных
Российская Федерация, Финансовый университет при Правительстве Российской Федерации
ESBudaev@fa.ru
Галкин Владимир Вячеславович
стажер исследователь института цифровых технологий факультета информационных технологий и анализа больших данных
Российская Федерация, Финансовый университет при Правительстве Российской Федерации
220943@edu.fa.ru

Аннотация

Статья посвящена задаче восстановления значений данных о межрегиональной миграции населения из агрегированных данных Росстата о числе прибывших и выбывших по всем регионам Российской Федерации. Для решения задачи строится система из 2N уравнений с N(N-1) неизвестными, где N – количество субъектов Федерации, и используется метод L_2 регуляризации, в котором дополнительно используются веса, обратно пропорциональные населению региона. Получено несколько решений с разными коэффициентами регуляризации. В результате восстанавливаются значения миграции между регионами по принципу «каждый с каждым». Коэффициент регуляризации α рекомендуется выбирать между значениями 10^(-1) и 10^(-3). Решение системы уравнений может дать отрицательные значения, и чтобы избежать этого рекомендуется переходить к задаче квадратичного программирования.

Ключевые слова

миграция, межрегиональная, регион, восстановление, имитационное моделирование миграции.

Финансирование

Статья подготовлена по результатам исследований, выполненных за счет бюджетных средств по государственному заданию Финуниверситета.

Рекомендуемая ссылка

Кораблев Юрий Александрович , Михайлова Светлана Сергеевна , Концевая Наталья Валерьевна , Будаев Евгений Сергеевич , Галкин Владимир Вячеславович

Метод восстановления данных по миграционной ситуации региона с использованием имитационного моделирования на основе агрегированных данных Росстата// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №2 (82). Номер статьи: 8201. Дата публикации: 28.04.2025. Режим доступа: https://eee-region.ru/article/8201/

Authors

Korablyov Yuriy Aleksandrovich
PhD in Economics, Research Fellow, Institute of Digital Technologies, Faculty of Information Technology and Big Data Analysis
Russian Federation, Financial University under the Government of the Russian Federation
YuAKorablev@fa.ru
Mikhailova Svetlana Sergeevna
PhD in Economics, Leading Research Fellow, Institute of Digital Technologies, Faculty of Information Technology and Big Data Analysis
Russian Federation, Financial University under the Government of the Russian Federation
SSMihajlova@fa.ru
Kontsevaya Natalya Valeryevna
PhD in Economics, Research Fellow, Institute of Digital Technologies, Faculty of Information Technology and Big Data Analysis
Russian Federation, Financial University under the Government of the Russian Federation
NVKontsevaya@fa.ru
Budaev Evgeny Sergeevich
PhD in Engineering, Research Fellow, Institute of Digital Technologies, Faculty of Information Technology and Big Data Analysis
Russian Federation, Financial University under the Government of the Russian Federation
ESBudaev@fa.ru
Galkin Vladimir Vyacheslavovich
Intern Researcher, Institute of Digital Technologies, Faculty of Information Technologies and Big Data Analysis
Russian Federation, Financial University under the Government of the Russian Federation
220943@edu.fa.ru

Abstract

The article is devoted to the task of restoring the values of data on interregional migration of the population from the aggregated data of Rosstat on the number of arrivals and departures in all regions of the Russian Federation. To solve the problem, a system of 2N equations with N(N-1) unknowns is constructed, where N is the number of subjects of the Federation, and the L_2 regularization method is used, which additionally uses weights inversely proportional to the population of the region. Several solutions with different regularization coefficients have been obtained. As a result, the values of migration between regions are restored according to the principle of "everyone with everyone". The regularization coefficient α is recommended to choose between the values 10^(-1) and 10^(-3). Solving a system of equations can give negative values, and to avoid this, it is recommended to proceed to the problem of quadratic programming.

Keywords

migration, interregional, region, recovery, migration simulation modeling.

Project finance

The article was prepared based on the results of research carried out at the expense of budgetary funds under a state assignment for the Financial University.

Suggested Citation

Korablyov Yuriy Aleksandrovich , Mikhailova Svetlana Sergeevna , Kontsevaya Natalya Valeryevna , Budaev Evgeny Sergeevich , Galkin Vladimir Vyacheslavovich

Method of data recovery on the migration situation of the region using simulation modeling based on Rosstat aggregated data// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №2 (82). Art. #8201. Date issued: 28.04.2025. Available at: https://eee-region.ru/article/8201/ 

Print Friendly, PDF & Email

Введение

Определение целей и стратегий развития регионов требует знания актуальной статистической информации. Ключевым показателем является численность населения, особенно, трудоспособного возраста. Существенное влияние на количественные показатели, да и на жизнь каждого отдельного региона, оказывает миграция населения. Миграция значительно участвует в формировании половозрастной структуры населения каждого субъекта Федерации. Умение предсказывать и управлять миграционными потоками будет способствовать более объективному планированию развития регионов. Поэтому исследование процессов миграции населения является актуальной задачей.

Одним из методов исследования является имитационное моделирование, которая может дать прогноз о том, например, какое ожидается изменение численности населения регионов в результате миграционных процессов в будущих годах. Благодаря современным программным средствам, таким как Anylogic, можно создать интерактивный интерфейс имитационной модели, который позволит выделить каждый из регионов, проваливаться внутрь (drill down/up) как в BI системах (системах бизнес-аналитики) (рис. 1), отобразить статистические данные, считанные из разных источников, наблюдать, как при изменении года происходит движение половозрастной диаграммы. Разрабатываемая имитационная модель предполагает использование агентно-ориентированного подхода, в котором с помощью диаграмм состояний задается логика функционирования агентов.

 

Вывод на экран половозрастной диаграммы населения для выбранного региона и для выбранного года

Рисунок 1 – Вывод на экран половозрастной диаграммы населения для выбранного региона и для выбранного года

 

Однако для построения агентно-ориентированной имитационной модели миграции населения необходимо выделить основные показатели, влияющие на принятие решения о миграции в тот или иной регион. И оказывается, что самая основная информация, сколько фактически переехало людей из одного субъекта Федерации в другой, в доступных статистических данных Росстата отсутствует. Данные Росстата отражают информацию только о том, сколько суммарно прибыло из других регионов или суммарно убыло людей в другие регионы (встречаются старые данные, и то только укрупненные по федеральным округам). В работах [1, 2, 3] упоминается использование матриц межрегиональной миграции, но так как сами работы и данные, по которым проводились исследования, являются достаточно старыми, то не нашлись сами источники данных. Без раздельных (не агрегированных) данных крайне затруднительно строить и проверять какие-либо закономерности. Поэтому данное исследование направлено на решение этой возникшей проблемы. По имеющимся агрегированным данным восстанавливаются данные миграции населения в разрезе каждого региона по принципу «каждый с каждым».

 

1. Агрегированные данные Росстата о миграционной ситуации регионов

На официальном сайте Росстата имеются агрегированные данные по миграции населения [4]. В таблице 1 для примера приведены данные за последние 10 лет (2014-2923) по Белгородской и Брянской областях.

 

Таблица 1 – Агрегированные данные Росстата за последние 10 лет

Таблица Росстата 2.10 Прибывшие Год Число прибывших из других
регионов России		 Таблица Росстата 2.10 Выбывшие Год Число прибывших из других
регионов России
всего в том числе в возрасте всего в том числе в возрасте
до 15  от 16 до 57(62) от 58(63) до 15  от 16 до 57(62) от 58(63)
Белгородская область 2023 16 539 2 936 10 978 2 625 Белгородская область 2023 19 338 2 940 13 560 2 552
2022 12 302 1 930 8 926 1 446 2022 19 258 3 193 15 299 2 880
2021 15 376 2 392 10 709 2 275 2021 16 327 3 025 14 918 2 635
2020 16 941 2 624 12 053 2 264 2020 16 390 2 747 14 097 2 476
2019 19 315 3 084 13 424 2 807 2019 19 052 2 682 14 941 2 317
2018 21 609 3 456 14 918 3 235 2018 21 372 2 388 13 983 1 982
2017 19 746 2 993 13 779 2 974 2017 20 578 2 068 8 527 1 199
2016 19 149 2 852 13 457 2 840 2016 19 320 2 280 9 804 1 158
2015 18 426 2 600 13 134 2 692 2015 19 940 2 063 9 129 1 196
2014 18 939 2 536 13 569 2 834 2014 18 353 1 965 9 226 1 154
Брянская область 2023 9 934 1 660 7 233 1 041 Брянская область 2023 11 794 2 688 11 621 1 363
2022 9 938 1 699 7 385 854 2022 13 242 3 135 13 369 1 557
2021 10 633 1 754 7 773 1 106 2021 12 388 2 740 12 864 1 445
2020 12 183 2 007 9 143 1 033 2020 12 345 2 530 12 038 1 439
2019 12 699 1 986 9 458 1 255 2019 15 672 2 451 13 506 1 384
2018 13 622 2 061 10 160 1 401 2018 18 061 2 116 12 967 1 262
2017 13 184 1 987 10 018 1 179 2017 17 049 2 940 13 560 2 552
2016 14 186 2 025 10 850 1 311 2016 16 007 3 193 15 299 2 880
2015 13 238 1 790 10 085 1 363 2015 17 341 3 025 14 918 2 635
2014 11 443 1 448 8 777 1 218 2014 16 345 2 747 14 097 2 476
… … … … … … … … … … … …

Источник: статистика Росстата [4].

 

В процессе исследования выявлено, что из 89 субъектов Российской Федерации в статистике Росстата имеются данные о миграционной ситуации по 85 субъектам, отсутствует информация по новым регионам – Донецкой Народной Республике, Луганской Народной Республике, Запорожской области и Херсонской области. По республике Крым и городу Севастополь отсутствуют данные за 2014 год. В таком случае отсутствующие данные можно исключить, либо заменить на нулевые, что может отрицательно отразиться на расчетах, либо же заменить их на обобщенные данные по миграции из новых регионов. Требуется из имеющихся агрегированных данных Росстата определить неагрегированные данные о межрегиональной миграции по принципу «каждый с каждым», как показано в таблице 2.

 

Таблица 2 – Данные миграции между регионами, подлежащие определению.

Миграция между регионами куда
Белгородская область Брянская область Владимирская область … Чукотский автономный округ
откуда Белгородская область — m12 m13 … m1N
Брянская

область

 m21 — m23 … m2N
Владимирская область m31 m32 — … m3N
… … … … … …
Чукотский автономный округ mN1 mN2 mN3 … —

 

Примечательно также, что общее число выбывших и общее число прибывших по всем регионам не совпадает. Так, например, в 2019 году число выбывших составляло 1 473 399 чел., а число прибывших – 1 473 332 чел. В 2023 году разница стала значительной, выбывших стало 1 212 297 чел., а прибывших – 1 268 633 чел. Скорее всего это объясняется невозможностью полного учета мигрирующих из новых регионов из-за продолжения военных действий. Эти несовпадения вносят в исследование некоторую специфику при попытке восстановить неагрегированные данные.

 

Метод восстановления нагрегированных данных о миграционной ситуации региона

Если рассматривать только данные одной возрастной группы или суммарные данные («всего»), то имеется  неизвестных N (N-1) и 2N уравнений вида:

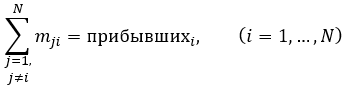                                                   (1)

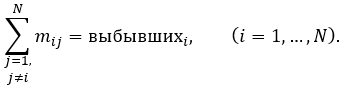                                                    (2)

где N – число субъектов, по которым имеются данные в статистике Росстата (всех будет 89, если поставить нулевые значения для новых регионов).

 

Количество переменных 89*88=7832 много больше количества уравнений 2*89=178. Матрица коэффициентов при неизвестных mij в системе уравнений будет выглядеть, как в таблице 3.

Приближенное решение может быть найдено при использовании регуляризации, например, L2 регуляризации. Оптимизационная задача тогда будет выглядеть иметь вид:

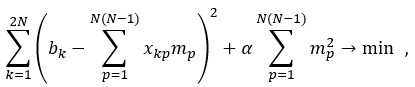                                                    (3)

где k – номер строки, а p – номер столбца в системе уравнений выше (для перехода от предыдущих индексов p=(N-1)*i-j )), α – коэффициент регуляризации.

 

Таблица 3 – Матрица коэффициентов при неизвестных mij и столбец известных значений

m12 m13 … m1N m21 m23 … m2N m31 m32 … … mN1 mN2 … mN(N-1) B
0 0 … 0 1 0 … 0 1 0 … … 1 0 … 0 b1
1 0 … 0 0 0 … 0 0 1 … … 0 1 … 0 b2
… … … … … … … … … … … … … … … … …
0 0 … 1 0 0 … 1 0 0 … … 0 0 … 0 bN
1 1 … 1 0 0 … 0 0 0 … … 0 0 … 0 bN+1
0 0 … 0 1 1 … 1 0 0 … … 0 0 … 0 bN+2
0 0 … 0 0 0 … 0 1 1 … … 0 0 … 0 bN+3
… … … … … … … … … … … … … … … … …
0 0 … 0 0 0 … 0 0 0 … … 1 1 … 1 b2N

Однако такая регуляризация будет одинаково влиять на все значения восстанавливаемых значений миграции независимо от количества населения самого региона, что кажется не логичным. Другими словами, значение mij  будет одинаково приглушаться в результате регуляризации как для крупного региона с большим населением, так и для небольшого региона с небольшим населением. Хочется учесть это и добавить соответствующие веса wp. Для регионов, откуда исходит миграция, этот вес должен быть обратно пропорционален количеству населения в регионе (количество населения в регионе берется также из данных Росстата):

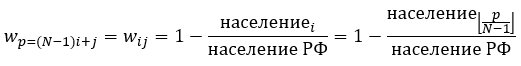                                                    (4)

Оптимизационная задача примет вид:

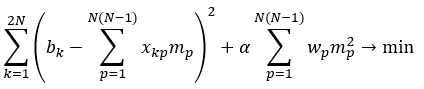                                                    (5)

Матричный вид этой задачи:

                                                    (6)

где   B=(b1, … , b2N)T    – вектор столбец правых частей уравнений;

X – матрица коэффициентов при неизвестных mp размерности (2N)×(N(N-1));

P=(m1, … , mN(N-1))T    – вектор столбец неизвестных mp;

W– диагональная матрица весов wp размерности (N(N-1))×(N(N-1)).

Решение данной оптимизационной задачи будет выражается формулой:

                                                    (7)

После расчета  можно для удобства собрать матрицу миграционных потоков между регионами с элементами mij , как показано в таблице 2.

 

2. Интерпретация результатов, вычисленных по методу восстановления неагрегированных данных

Результат зависит от величины коэффициента регуляризации α. Сама регуляризация, перетягивая часть невязки наблюдений на себя, делает оценки неизвестных параметров смещенными, но в то же время, более стабильными. Напомним, что сами исходные данные могут содержать неточность. Результат также зависит от способа борьбы с отсутствующими данными. Для примера рассмотрим результаты расчетов миграции по всем возрастным группам Воронежской области для 2022 года, что приведено в таблице 4. При коэффициенте регуляризации α=0 ожидаемое решение не находится, получающаяся матрица оказывается сингулярной. При α=1 имеем решение, но регуляризация оказывает достаточно сильное влияние, например, суммарное по всем регионам количество прибывших становится заниженным почти на 10 000 человек (1 810 827 против 1 821 051). При α=0.01 все еще занижено почти на 1 000, но для одного региона разница лишь около 10 человек. При α=0.001 суммарное количество по всем регионам отличается лишь на 10, для одного региона менее чем на единицу. Дальнейшее уменьшение коэффициента регуляризации нецелесообразно, все равно дробные части нас не интересуют, и придется использовать округление.

 

Таблица 4 – Расчет потока миграции в 2022 году для субъекта Воронежская область (по всем возрастным группам).

Воронежская область α=10-0 α=10-1 α=10-3 α=10-9
Прибывших Выбывших Прибывших Выбывших Прибывших Выбывших Прибывших Выбывших
всего факт 22334 22142 22334 22142 22334 22142 22334 22142
всего расчет 22196 22006 22320 22128 22333 22141 22334 22142
регионы из в из в из в из в
Белгородская область 238,72 108,57 239,98 107,86 240,12 107,78 240,07 107,59
Брянская область 170,63 132,73 171,20 132,92 171,26 132,94 171,21 132,90
Владимировская область 212,04 169,00 213,03 169,57 213,14 169,63 213,07 169,64
Воронежская область — — — — — — — —
Ивановская область 154,28 127,76 154,67 127,90 154,71 127,91 154,64 127,82
Калужская область 213,28 213,20 214,31 214,22 214,42 214,33 214,35 214,27
Костромская область 108,66 93,05 108,60 92,83 108,59 92,81 108,53 92,73
Курская область 168,26 135,70 168,83 135,92 168,89 135,95 168,81 135,87
Липецкая область 143,41 128,94 143,52 129,09 143,53 129,10 143,49 129,01
Московская область 1817,64 2362,68 1835,32 2385,85 1837,29 2388,43 1837,13 2389,46
Орловская область 93,86 80,77 93,45 80,43 93,41 80,39 93,42 80,33
Рязанская область 175,00 160,27 175,64 160,75 175,71 160,80 175,63 160,76
Смоленская область 157,53 129,64 157,97 129,80 158,02 129,81 157,97 129,79
Тамбовская область 156,15 121,60 156,58 121,68 156,62 121,68 156,56 121,68
Тверская область 217,85 183,48 218,91 184,20 219,03 184,28 218,95 184,30
Тульская область 216,48 179,35 217,53 180,03 217,65 180,10 217,59 180,07
Ярославская область 150,94 164,43 151,09 164,94 151,11 165,00 150,98 164,95
г. Москва 2052,56 2939,68 2072,71 2968,77 2074,95 2972,01 2074,66 2972,84
Республика Карелия 75,66 97,03 75,04 96,85 74,97 96,82 74,99 96,80
Республика Коми 194,16 136,31 195,01 136,54 195,11 136,56 195,12 136,50
Ненецкий автономный округ 31,61 29,24 30,75 28,36 30,65 28,26 30,71 28,13
Архангельская область 192,48 160,82 193,30 161,30 193,39 161,35 193,42 161,34
Вологодская область 138,35 113,56 138,59 113,55 138,62 113,55 138,61 113,53
Калининградская область 169,75 219,66 170,29 220,74 170,35 220,86 170,33 220,83
Ленинградская область 555,01 886,51 559,60 894,45 560,11 895,33 560,23 895,35
Мурманская область 258,01 221,98 259,45 223,09 259,61 223,22 259,64 223,25
Новгородская область 125,26 118,41 125,37 118,45 125,38 118,45 125,40 118,38
Псковская область 135,43 121,16 135,52 121,23 135,53 121,24 135,52 121,20
г.Санкт-Петербург 1244,45 1259,88 1256,14 1271,72 1257,44 1273,03 1257,72 1273,16
Республика Адыгея 112,16 158,17 112,03 158,62 112,01 158,66 111,97 158,65
Республика Калмыкия 95,98 83,07 95,71 82,74 95,68 82,71 95,69 82,62
Краснодарский край 896,99 989,29 905,10 998,32 906,01 999,33 906,19 999,58
Астраханская область 155,30 114,56 155,61 114,56 155,65 114,56 155,59 114,54
Волгоградская область 325,38 273,81 327,53 275,47 327,76 275,65 327,88 275,58
Ростовская область 475,78 402,17 479,48 405,15 479,89 405,48 480,02 405,44
Республика Крым 257,80 229,07 259,25 230,25 259,41 230,38 259,38 230,39
г. Севастополь 135,37 225,87 135,57 227,01 135,59 227,14 135,54 227,16
Республика Дагестан 338,45 305,20 340,78 307,17 341,04 307,39 341,10 307,38
Республика Ингушетия 62,06 75,93 61,51 75,53 61,45 75,49 61,53 75,40
Кабардино-Балкарская Республика 106,23 81,34 106,16 81,00 106,16 80,96 106,18 80,89
Карачаево-Черкесская Республика 85,55 73,14 85,26 72,72 85,23 72,67 85,28 72,64
Республика Северная Осетия-Алания 120,68 68,36 120,76 67,89 120,76 67,83 120,78 67,75
Чеченская Республика 159,35 100,77 159,79 100,63 159,84 100,62 159,77 100,50
Ставропольский край 382,24 395,13 384,98 398,03 385,28 398,35 385,34 398,34
Республика Башкортостан 464,05 442,64 467,64 446,04 468,04 446,41 468,09 446,40
Республика Марий Эл 109,53 103,51 109,45 103,40 109,45 103,39 109,43 103,35
Республика Мордовия 135,33 106,02 135,53 105,93 135,56 105,92 135,53 105,82
Республика Татарстан 283,91 322,87 285,68 325,01 285,87 325,25 285,85 325,21
Удмуртская Республика 163,73 145,35 164,22 145,67 164,28 145,70 164,23 145,59
Чувашская Республика 171,71 50,81 172,31 49,49 172,37 49,35 172,36 49,24
Пермский край 234,54 182,12 235,78 182,82 235,92 182,90 235,93 182,85
Кировская область 174,33 162,26 174,94 162,76 175,00 162,81 174,92 162,81
Нижегородская область 256,48 249,77 257,94 251,17 258,10 251,32 258,08 251,27
Оренбургская область 268,78 179,79 270,36 180,47 270,54 180,55 270,49 180,51
Пензенская область 149,95 123,76 150,29 123,86 150,33 123,87 150,30 123,82
Самарская область 286,06 271,77 287,82 273,39 288,02 273,57 288,03 273,59
Саратовская область 295,72 228,78 297,58 229,97 297,78 230,10 297,86 230,15
Ульяновская область 162,88 126,85 163,36 126,99 163,42 127,00 163,37 126,98
Курганская область 164,34 129,89 164,83 130,06 164,88 130,07 164,85 130,01
Свердловская область 394,39 343,41 397,29 345,78 397,61 346,04 397,64 346,10
Тюменская область 166,35 179,13 166,84 179,79 166,89 179,87 166,85 179,89
Ханты-Мансийский автономный округ-Югра 421,73 409,94 424,90 413,00 425,26 413,34 425,27 413,49
Ямало-Ненецкий автономный округ 214,98 200,33 215,97 201,21 216,08 201,31 216,06 201,31
Челябинская область 364,76 336,29 367,35 338,59 367,64 338,84 367,68 338,93
Республика Алтай 67,12 64,36 66,61 63,84 66,55 63,79 66,62 63,74
Республика Бурятия 175,40 148,71 176,05 149,07 176,12 149,11 176,09 149,11
Республика Тыва 86,54 65,16 86,25 64,66 86,22 64,60 86,32 64,59
Республика Хакасия 134,27 125,59 134,47 125,70 134,49 125,72 134,50 125,69
Алтайский край 282,75 237,30 284,49 238,58 284,69 238,72 284,67 238,80
Забайкальский край 168,54 111,24 169,05 111,22 169,11 111,21 169,07 111,20
Красноярский край 429,71 429,37 432,96 432,62 433,32 432,98 433,27 433,19
Иркутская область 269,38 188,16 270,93 188,93 271,10 189,02 271,09 189,02
Кемеровская область 317,70 238,56 319,76 239,85 319,99 239,99 320,06 240,10
Новосибирская область 333,58 320,58 335,82 322,71 336,07 322,95 336,11 323,08
Oмская область 246,87 164,16 248,21 164,68 248,36 164,74 248,36 164,76
Томская область 168,85 130,56 169,40 130,73 169,46 130,75 169,43 130,75
Республика Саха (Якутия) 178,49 141,65 179,16 141,93 179,23 141,96 179,18 141,96
Камчатский край 101,77 95,08 101,63 94,88 101,61 94,85 101,69 94,88
Приморский край 260,58 207,60 262,08 208,57 262,25 208,68 262,20 208,77
Хабаровский край 251,84 215,35 253,25 216,39 253,41 216,51 253,41 216,59
Амурская область 146,44 120,05 146,77 120,11 146,81 120,12 146,80 120,15
Магаданская область 70,24 57,55 69,80 56,97 69,75 56,90 69,83 56,86
Сахалинская область 116,77 91,56 116,81 91,33 116,82 91,30 116,87 91,25
Еврейская автономная область 64,60 47,04 64,10 46,35 64,05 46,27 64,14 46,18
Чукотский автономный округ 66,40 62,51 65,94 61,97 65,88 61,91 65,97 61,83
Донецкая Народная Республика 24,61 19,42 23,71 18,44 23,61 18,33 23,70 18,22
Луганская Народная Республика 25,08 19,43 24,19 18,45 24,09 18,34 24,17 18,22
Запорожская область 25,09 19,43 24,21 18,45 24,11 18,34 24,19 18,25
Херсонская область 23,43 19,41 22,50 18,43 22,40 18,32 22,48 18,19

 

Подходящим вариантом видится выбор коэффициента регуляризации между 0.1 и 0.001, когда разница между расчетным и фактическим количеством прибывших или выбывших человек отличается незначительно, и в то же время неточности в исходных данных не будут приводить к значительным изменениям.

Одним из недостатков такого решения является возможность получения отрицательных значений для количества прибывших или выбывших. Например, расчет для 2022 года показал, что в Белгородскую область прибыло из Брянской области минус 30 людей. Очевидно, что количество прибывших не должно быть отрицательным. Конечно же, это можно исправить на соответствующую величину, тогда следует увеличить поток выбывших в указанный регион. Однако при таком ручном исправлении система уравнений не будет согласованной. Другим решением является добавление условия неотрицательности переменных P≥0 к оптимизационной задаче, представленной формулой (6). В этом случае мы приходим к задаче квадратичного программирования, которая решается чуть сложнее. Следует использовать итеративные алгоритмы, такие как метод Лемке для решения задач линейной дополнительности [5] (хорошее объяснение дается в источнике [6], а в работе [7] в сопроводительных материалах есть реализация на Python) или метод внутренней точки [8], который используется во многих пакетах оптимизации [9]. Однако это уже тема для другого исследования.

В любом случае, мы получили всего лишь восстановленные данные. На самом деле в реальности ситуация могла быть совсем другой. К сожалению, актуальные и детальные данные по миграции между регионами не публикуются, сверить результаты с ними мы не можем, а если бы публиковались, то и смысла проводить эти расчеты не было бы. Эти данные нужны для проведения дальнейших настройки и отладки механизмов разрабатываемой имитационной модели. Если будут когда-то известны реальные значения миграции между регионами, то не составит труда запустить модель с ними. А до того, преимущественно для целей разработки и отладки, мы вынуждены использовать их. Само получившееся исследование может быть интересным с точки зрения демонстрации результатов попытки восстановления миграции между регионами.

 

Заключение

В результате исследования получены формулы в матричном виде для восстановления детальной информации по миграции между регионами из агрегированных данных о суммарном количестве прибывших/выбывших в/из региона. Для N=89 регионов имеем систему из 2N=178 уравнений с N(N-1)=7832 переменным. Для получения решения используется L2 регуляризация с дополнительными весами, обратно пропорциональными населению регионов. Решение дает приближенный результат. Коэффициент регуляризации рекомендуется выбирать между α=10-1 и α=10-3.  Восстановленные значения миграции между некоторыми регионами при решении системы линейных уравнений могут оказаться отрицательными. Для исправления следует либо изменять противоположный поток на соответствующую величину, или же добавлять условия неотрицательности переменных и переходить к задаче квадратичного программирования. Восстановленные данные по миграции между регионами используются для разработки и отладки имитационной модели.

 

Список литературы

  1. Вакуленко, Е.С., Мкртчян, Н.В., Фурманов К.К. Моделирование регистрируемых миграционных потоков между регионами Российской Федерации / Е.С. Вакуленко, Н.В. Мкртчян, К.К. Фурманов // Прикладная эконометрика. – 2011. – № 1 (21). – С. 35-55.
  2. Mkrtchyan, N., Vakulenko, E. Interregional migration in Russia at different stages of the life cycle / N. Mkrtchyan N., E. Vakulenko E. // GeoJournal. –2019. – V. 84, № 6. – P. 1549-1565.
  3. Kumo, К. Inter-regional Population Migration in Russia: Using an Origin-to-Destination Matrix // Post-Communist Economies. – 2007. – Vol. 19, № 2. – 131–152. – DOI: 10.1080/14631370701312022
  4. Численность и миграция населения Российской Федерации: Федеральная служба государственной статистики (Росстат) [Электронный ресурс]. – URL: https://rosstat.gov.ru/compendium/document/13283 (Дата обращения 15.02.2025)
  5. Katta, G.M. 2006. Linear complementarity linear and nonlinear programming. Internet Edition. / G.M. Katta, Feng-Tien Yu. – 2006. – 629 p. – Текст : электронный. – URL: https://web.archive.org/web/20100605193200if_/http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/ (дата обращения: 10.03.2024)
  6. Писарук, Н.Н. 2014. Исследование операций / Н.Н. Писарук. – Минск : Белорусский Государственный Университет, 2014. – 289 с.
  7. Korablev, Yu.A. Monotone smoothing cubic spline and spline collocation for restoring the product consumption rate and predicting events (FunctionalSmoothingSpline), 20 August 2024, PREPRINT (Version 1), available at Research Square. – URL: https://doi.org/10.21203/rs.3.rs-4742025/v1 (дата обращения: 15.02.2025)
  8. Дикин, И. И. Итеративное решение задач линейного и квадратичного программирования // Докл. АН СССР. — 1967. — Т. 174, № 4. — С. 747—748.
  9. Caron, S. Quadratic programming in Python : [сайт] / Stéphane Caron Blog. – Текст : электронный. – URL: https://scaron.info/blog/quadratic-programming-in-python.html (дата обращения: 15.02.2025)

 

References

  1. Vakulenko, E.S., Mkrtchyan, N.V., Furmanov, K.K. Modeling registered migration flows between the regions of the Russian Federation. [Modelirovanie registriruemykh migratsionnykh potokov mezhdu regionami Rossiyskoy Federatsii] / E.S. Vakulenko, N.V. Mkrtchyan, K.K. Furmanov // Prikladnaya ekonometrika, 2011. – No. 1 (21). – P. 35-55.
  2. Mkrtchyan, N., Vakulenko, E. Interregional migration in Russia at different stages of the life cycle / N. Mkrtchyan N., E. Vakulenko E. // GeoJournal. –2019. – V. 84, № 6. – P. 1549-1565.
  3. Kumo, К. Inter-regional Population Migration in Russia: Using an Origin-to-Destination Matrix // Post-Communist Economies. – 2007. – Vol. 19, № 2. – 131–152. – DOI: 10.1080/14631370701312022
  4. Federal State Statistics Service (Rosstat). Population and Migration of the Russian Federation. [Chislennost’ i migratsiya naseleniya Rossiyskoy Federatsii: Federal’naya sluzhba gosudarstvennoy statistiki (Rosstat)] // Federal State Statistics Service (Rosstat). – URL: https://rosstat.gov.ru/compendium/document/13283(Accessed: February 15, 2025).
  5. Katta, G.M. 2006. Linear complementarity linear and nonlinear programming. Internet Edition. / G.M. Katta, Feng-Tien Yu. – 2006. – 629 p. – Текст : электронный. – URL: https://web.archive.org/web/20100605193200if_/http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/ (дата обращения: 10.03.2024)
  6. Pisaryuk, N.N. Operations Research. [Issledovanie operatsiy] / N.N. Pisaryuk // Belarusian State University, 2014. — 289 p.
  7. Korablev, Yu.A. Monotone smoothing cubic spline and spline collocation for restoring the product consumption rate and predicting events (FunctionalSmoothingSpline), 20 August 2024, PREPRINT (Version 1), available at Research Square. – URL: https://doi.org/10.21203/rs.3.rs-4742025/v1 (дата обращения: 15.02.2025)
  8. Dikin, I. I. Iterative solution of problems of linear and quadratic programming. [Iterativnoe reshenie zadach lineynogo i kvadratichnogo programmirovaniya] // Dokl. AN SSSR, 1967. — Vol. 174, No. 4. — P. 747—748.
  9. Caron, S. Quadratic programming in Python : [сайт] / Stéphane Caron Blog. – Текст : электронный. – URL: https://scaron.info/blog/quadratic-programming-in-python.html (дата обращения: 15.02.2025)

Еще в рубриках

Регионы России

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *