Оценка структурной сложности региональных экономик и ее влияния на ВРП
Assessment of the structural complexity of regional economies and its impact on GRP
Авторы
Аннотация
Целью данной работы является построение интегрального индекса структурной сложности на основе четырех базовых индексов сложности региональных экономик: индекс сложности структур ВРП по данным об объемах производства по видам экономической деятельности (ВЭД); индекс сложности структур занятости регионов по профгруппам; индекс сложности структур занятости регионов по ВЭД; индекс сложности структур распределения предприятий в регионах по ВЭД. Построены четыре интегральных индекса структурной сложности региональных экономик. Показано, что структурная сложность региональной экономики оказывает влияние на ВРП. Получены оценки эластичности ВРП по интегральному индексу структурной сложности.
Интегральный индекс структурной сложности региональных экономик позволяет комплексно оценить экономический потенциал территорий, выявить наиболее перспективные отрасли и производства, а также обозначить направления диверсификации, которые способствуют укреплению экономической безопасности регионов в условиях санкционного давления. Это создает основу для формирования обоснованных стратегий пространственного развития, ориентированных на повышение экономической сложности и устойчивости региональных экономик.
Ключевые слова
региональная экономика, эконометрика, экономическая сложность, интегральный индекс.
Рекомендуемая ссылка
Оценка структурной сложности региональных экономик и ее влияния на ВРП// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №2 (82). Номер статьи: 8205. Дата публикации: 15.06.2025. Режим доступа: https://eee-region.ru/article/8205/
Authors
Abstract
The purpose of this work is to build an integral index of structural complexity based on four basic indices of complexity of regional economies: the index of complexity of GRP structures according to data on production volumes by type of economic activity (TEA); the index of complexity of employment structures of regions by professional groups; the index of complexity of employment structures of regions according to TEA; the index of complexity of structures of distribution of enterprises in regions. Four integral indices of the structural complexity of regional economies have been constructed. It is shown that the structural complexity of the regional economy has an impact on GRP. Estimates of the elasticity of GRP according to the integral index of structural complexity are obtained.
The integral index of the structural complexity of regional economies makes it possible to comprehensively assess the economic potential of territories, identify the most promising industries and industries, as well as identify areas of diversification that contribute to strengthening the economic security of regions under sanctions pressure. This creates the basis for the formation of sound spatial development strategies aimed at increasing the economic complexity and sustainability of regional economies.
Keywords
regional economics, econometrics, economic complexity, integral index.
Suggested Citation
Assessment of the structural complexity of regional economies and its impact on GRP// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №2 (82). Art. #8205. Date issued: 15.06.2025. Available at: https://eee-region.ru/article/8205/
Введение
Укрепление экономической безопасности регионов в условиях санкционного давления предполагает повышение сложности производственных структур и экономических систем. Рекомендации по диверсификации национальной и региональных экономик могут быть основаны на подходах, ориентированных на повышение экономической сложности (Афанасьев, Кудров, 2021; Hidalgo, Hausmann, 2009). В настоящее время исследованы возможности оценки экономической сложности региональных экономик по данным об объемах экспорта и объемах производства продуктов, о численности занятых в различных отраслях экономики (Афанасьев, Гусев, 2023; Афанасьев и др., 2023). Индексы экономической сложности используются для обоснования приоритетных направлений диверсификации. Например, в работе (Афанасьев, Ильин, 2022) предложен подход к выбору направлений диверсификации на основе рекомендаций по развитию секторов, направленный на повышение экономической сложности региональной экономики. Накопленный опыт построения индексов экономической сложности позволяет подойти к решению задачи обобщенной оценки сложности региональных экономик с использованием интегрального индекса структурной сложности. Построение такого индекса и анализ возможностей его использования является целью данной работы. Для построения интегрального индекса авторами сформированы различные структуры региональной экономики: структура ВРП по данным об объемах производства по ВЭД; структура занятости регионов по профгруппам; структура занятости регионов по ВЭД; структура распределения предприятий по ВЭД. Базовые индексы, составляющих информационную основу для построения интегральных индексов, представлены в ранее опубликованных работах авторов.
Подход к оценке сложности структур профессиональной занятости регионов описан в работе (Афанасьев и др., 2023). Для построения индекса ZPRF – сложности структур занятости регионов по профгруппам использованы данные Росстата о списочной численности работников организаций по 11 профессиональным группам в субъектах РФ за 2022г.: «О численности и потребности организаций в работниках по профессиональным группам» (Росстат: О численности и потребности организаций в работниках по профессиональным группам. URL: https://rosstat.gov.ru/compendium/document/13266 (дата обращения 15.08.2024)). Нормированный индекс ZPRF со значениями в интервале [0; 1] приведен в столбце (4) таблицы П1 приложения. Для построения индекса ZV сложности структур занятости регионов по 14 ВЭД использованы данные Росстата «распределение среднегодовой численности занятых по видам экономической деятельности» (ЕМИСС: Среднегодовая численность занятых в экономике (расчеты на основе интеграции данных) с 2017 г. URL: https://www.fedstat.ru/indicator/58994 (дата обращения 15.03.2024)) за 2022 г. Нормированный индекс ZV приведен в столбце (5) таблицы П1 приложения. Схема расчета и анализ индекса VRPV сложности структур ВРП по данным об объемах производства по ВЭД описаны в работе (Гусев, 2025). Для оценки экономической сложности 85 регионов использованы показатели структуры ВРП в ценах 2016 г. по 19 ВЭД за 2022 г. из ЕМИСС: «Валовой региональный продукт (в постоянных ценах 2016 года; тыс. руб.)» (ЕМИСС: Валовой региональный продукт в основных ценах (ОКВЭД 2). URL: https://www.fedstat.ru/indicator/61497 (дата обращения 20.03.2024)). Нормированный индекс VRPV приведен в столбце (3) таблицы П1 приложения. На основе показателя Росстата «распределение числа предприятий и организаций по видам экономической деятельности (на конец года)» (Росстат: Регионы России. Социально-экономические показатели. URL: https://rosstat.gov.ru/folder/210/document/13204 (дата обращения 20.08.2024)) по 19 ВЭД за 2022 г. в соответствии с методологией оценки экономической сложности рассчитан индекс PRV сложности структур распределения предприятий в регионах по ВЭД. Нормированный индекс PRV приведен в столбце (6) таблицы П1 приложения.
Интегральные индексы структурной сложности экономики
Предварительные этапы расчетов интегральных индексов
Далее будут рассмотрены четыре подхода к построению интегральных индексов сложности структур региональных экономик с использованием базовых индексов. Для каждого подхода требуется выполнение двух предварительных расчетных этапов, указанных ниже:
Этап 1. Вначале производится расчет 4 базовых индексов сложности:
- VRPV — индекс сложности структур ВРП по данным об объемах производства по ВЭД;
- ZPRF — индекс сложности структур занятости регионов по профгруппам;
- ZV — индекс сложности структур занятости регионов по ВЭД;
- PRV — индекс сложности структур распределения предприятий в регионах по ВЭД.
Этап 2. Далее проводится нормирование каждого базового индекса:
Пусть IND – один из базовых индексов сложности, рассчитанный на этапе 1 с компонентами (IND1 , …, INDk , …, INDN). Здесь N – число регионов, k – номер региона, INDk – компонента индекса, соответствующая региону k. Пусть maxIND – максимальное значение компонент индекса, minIND – минимальное значение компонент индекса. Компоненты nINDk нормированного индекса nIND рассчитываются по формуле:
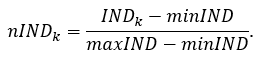
Компоненты каждого нормированного базового индекса сложности nVRPV, nZPRF, nZV, nPRV принимают значения в интервале [0; 1]. Нормированные базовые индексы, построенные по данным 2022 года, представлены в столбцах (3)-(6) таблицы П1 приложения.
Подходы к построению интегральных индексов и результаты по данным 2022 года.
Интегральный индекс INT1.
Первый подход заключается в построении интегрального индекса INT1 по методу главных компонент с использованием базовых индексов. Собственные значения корреляционной матрицы базовых индексов 2,23; 1,04; 0,38; 0,36. Первая главная компонента объясняет 55,68% общей дисперсии четырех базовых индексов. Этого достаточно, чтобы рассматривать первую главную компоненту в качестве интегрального индекса (Айвазян, 2012, С. 98). Индекс INT1 может быть представлен в виде линейной функции нормированных базовых индексов (1) со значениями коэффициентов, приведенными в таблице 1:
![]() (3)
(3)
В таблице 1 представлены коэффициенты функции (1) для нормированного интегрального индекса nINT1. Коэффициенты корреляции индексов nINT1 и INT1 с базовыми индексами указаны в таблице 2. Поскольку используемое нами нормирование индекса является линейным преобразованием, то оно не меняет значения коэффициентов корреляций. Индекс nINT1 приведен в столбце (7) таблицы П1 приложения. Регионы в столбце (2) этой таблицы упорядочены по убыванию значений компонент индекса nINT1. В столбце (1) таблицы П1 приложения – ранги регионов по индексу nINT1.
Таблица 1. Весовые коэффициенты интегральных индексов.
| a | b | c | d | const | |
| INT1 | 2,7651 | 2,4972 | 2,2116 | 3,2487 | -4,0314 |
| nINT1 | 0,3228 | 0,2914 | 0,2581 | 0,3792 | -0,2330 |
| INT2 | 0,25 | 0,25 | 0,25 | 0,25 | |
| nINT2 | 0,3137 | 0,3137 | 0,3137 | 0,3137 | -0,2348 |
| INT3 | 0,4729 | 0,0609 | 0,2887 | 0,1775 | |
| nINT3 | 0,5733 | 0,0738 | 0,3500 | 0,2152 | -0,2077 |
| nINT4 | 0,2497*** | 0,2766*** | 0,2910*** | 0,3959*** | -0,1961*** |
***значимость оценки на 1%-м уровне
Интегральный индекс INT2.
Рассмотрим второй подход к построению интегрального индекса (INT2). INT2 рассчитывается по формуле (3) с равными весовыми коэффициентами при нормированных базовых индексах a=b=c=d=0.25 и const=0. Назовем INT2 индексом «равных вложений» базовых индексов (см. в таблице П1 приложения указаны значения нормированного индекса в столбце (8), а ранги регионов по индексу nINT2 в столбце (11)). Коэффициенты корреляции индексов nINT2 и INT2 с базовыми индексами указаны в таблице 2.
Таблица 2. Коэффициенты корреляции интегральных и базовых индексов.
| nVRPV | nZPRF | nZV | nPRV | |
| nINT1 | 0,6138 | 0,8317 | 0,7071 | 0,8116 |
| nINT2 | 0,6018 | 0,8359 | 0,7345 | 0,7876 |
| nINT3 | 0,7237 | 0,7237 | 0,7237 | 0,7237 |
| nINT4 | 0,5524 | 0,8060 | 0,7486 | 0,8318 |
Интегральный индекс INT3.
В третьем подходе при расчете интегрального индекса INT3 по формуле (3) при const=0 весовые коэффициенты подобраны таким образом, что коэффициенты корреляции интегрального индекса INT3 с базовыми индексами равны. Значения весовых коэффициентов указаны в таблице 1. Такой интегральный индекс можно назвать индексом «равных влияний» базовых индексов. В таблице П1 приложения указан нормированный индекс nINT3 в столбце (9), а ранги регионов по индексу nINT3 в столбце (12). В таблице 1 приведены коэффициенты функции (1) для индекса nINT3. В таблице 2 – коэффициенты корреляции индексов nINT3 и INT3 с базовыми индексами.
Расчет индекса INT3 проводится по следующей пошаговой процедуре:
Шаг 1. Для const=0 и произвольных положительных значений коэффициентов (например, a=b=c=d=1), рассчитываются компоненты индекса INT3 по формуле (1).
Шаг 2. Рассчитываются коэффициенты корреляции каждого нормированного базового индекса сложности с индексом INT3. Если все коэффициенты корреляции равны между собой с заданным уровнем точности, то переходим к шагу 4.
Шаг 3. Изменяются весовые коэффициенты в формуле (1). Увеличивается значение весового коэффициента для базового индекса сложности, у которого коэффициент корреляции с интегральным индексом имеет минимальное значение, или уменьшается значение весового коэффициента при базовом индексе, у которого коэффициент корреляции с интегральным индексом имеет максимальное значение (Если корреляция базовых индексов с интегральным индексом, рассчитанным по формуле (1), положительная, то увеличение (уменьшение) весового коэффициента при этом индексе в формуле (1) приводит к увеличению (уменьшению) коэффициента корреляции этого индекса с интегральным. В Excel при четырех базовых индексах расчет интегрального индекса занимает несколько минут.). Переходим к шагу 2.
Шаг 4. Нормируем весовые коэффициенты так, чтобы a+b+c+d=1. Рассчитываем интегральный индекс INT3 по формуле (1) с нормированными весовыми коэффициентами.
Интегральный индекс INT4.
В основе четвертого подхода лежит идея построения индекса, изложенная в монографии (Айвазян, 2012, С. 103) и основанная на измерении расстояния от точки с координатами (nVRPVk, nZPRFk, nZVk, nPRVk), соответствующей каждому региону k в пространстве нормированных базовых индексов, до точки – «эталона» с координатами (1; 1; 1; 1).
Это расстояние равно:
![]()
Нормируем расстояния, рассчитанные для всех регионов, по формуле:
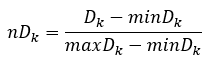
Рассчитываем значение компоненты индекса INT4 по формуле: INT4k = 1 — nDk. Чем меньше расстояние от точки (nVRPVk, nZPRFk, nZVk, nPRVk), характеризующей регион k в пространстве базовых индексов, до эталона, тем выше значение компоненты индекса INT4. При этом компоненты индекса INT4 принимают значения в интервале [0; 1]. В таблице П1 приложения указан нормированный индекс nINT4 в столбце (10), а в столбце (12) – ранги регионов по индексу nINT4. Индекс nINT4 не может быть представлен в виде линейной зависимости (3) от нормированных базовых индексов. В последней строке таблицы 1 приведены оценки коэффициентов линейной регрессии индекса nINT4 на нормированные базовые индексы. Все оценки значимы на 1%-м уровне. Коэффициент детерминации R2=0.994. Коэффициенты корреляции с базовыми индексами указаны в таблице 2.
Оценка влияния структурной сложности на ВРП
В ряде зарубежных публикаций (Hartmann, 2017; Hidalgo, 2021) показано, что сложность экономики оказывает влияние на ВВП, уровень неравенства в распределении доходов, социально-экономическое развитие национальных экономик. В данном разделе мы оценим влияние структурной сложности экономики на ВРП российских регионов. При этом мы исходим из того, что структурная сложность не только является фактором ВРП, но и оказывает на него непосредственное влияние.
Включим интегральный индекс в степенную производственную функцию
![]() (4)
(4)
где Lk – численность занятых, Kk – стоимость основных фондов в регионе k.
Коэффициент детерминации R2 регрессии (4) с каждым из четырех интегральных индексов превосходит 0,959. Но оценки коэффициентов при интегральных индексах для совокупности 85 регионов незначимы.
Для большинства регионов характерна экспоненциальная зависимость ВРП от значений интегральных индексов, подтвержденная оценками в таблице 3. В то же время для некоторых регионов с малыми значениями интегрального индекса nINT эта зависимость нарушается из-за несоответствия относительно высокого объема ВРП относительно низкому значению интегрального индекса. Для этих регионов можно указать факторы, которые разнонаправленно влияют на ВРП и структурную сложность. Например, природная рента (В соответствии с общепринятым подходом в качестве природной ренты рассматривается дополнительный ВРП, получаемый сверх обусловленного затратами производственных факторов.). В ряде исследований приводятся оценки природной ренты некоторых регионов, специализирующихся в области добычи нефти и природного газа. Например, оценки доли природной ренты в ВРП, полученные в (Айвазян и др., 2018) превышают 20% ВРП, а для некоторых регионов достигают 40%. Это является причиной диспропорции между интегральными оценками структурной сложности экономик и ВРП. К регионам, специализирующимся на добыче нефти и природного газа (Афанасьев, Гусев, 2023) и вносящим наибольший вклад в суммарный ВРП российских регионов, относятся: Ханты-Мансийский автономный округ, Ямало-Ненецкий автономный округ, Ненецкий автономный округ, Красноярский край, Республика Татарстан, Республика Саха (Якутия), Оренбургская область, Иркутская область.
Исключение из рассмотрения этих регионов приводит к росту эластичности ВРП по труду и снижению эластичности ВРП по капиталу в производственной функции, оцененной без учета интегрального индекса (см. оценки в столбцах (2) и (3) таблицы 3). Это соответствует результатам оценки коэффициентов эластичности в работе (Айвазян и др., 2016) для добывающих и равномерно развитых регионов. Оценки коэффициентов при интегральных индексах nINT1, nINT2 и nINT4 (столбцы (4), (5), (7) табл.3) в производственной функции (4) значимы на 5% -м уровне. Оценка коэффициента при nINT3 незначима.
Таблица 3. Оценки параметров функции (4) для 77 регионов
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| nINT1 | nINT2 | nINT3 | nINT4 | |||
| α t-статистика p-значение |
0,177*** (4,10) 0,000 |
0,336*** (5,44) 0,000 |
0,319*** (5,28) 0,000 |
0,322*** (5,31) 0,000 |
0,327*** (5,33) 0,000 |
0,325*** (5,44) 0,000 |
| β t-статистика p-значение |
0,8137*** (21,51) 0,000 |
0,667*** (12,54) 0,000 |
0,651*** (12,45) 0,000 |
0,651*** (12,39) 0,000 |
0,651*** (12,06) 0,000 |
0,641*** (12,24) 0,000 |
| s t-статистика p-значение |
0,378** (2,28) 0,025 |
0,365** (2,12) 0,037 |
0,317 (1,50) 0,138 |
0,416** (2,53) 0,014 |
||
| const t-статистика p-значение |
5,698*** (18,65) 0,000 |
5,718*** (16,33) 0,000 |
6,080*** (16,19) 0,000 |
6,045*** (16,11) 0,000 |
5,957*** (15,59) 0,000 |
6,138*** (16,30) 0,000 |
| N | 85 | 77 | 77 | 77 | 77 | 77 |
| R2 | 0,9660 | 0,9585 | 0,9613 | 0,9609 | 0,9597 | 0,9618 |
***значимость оценки на 1%-м уровне
**значимость оценки на 5%-м уровне
Эластичность ВРП региона k по интегральному индексу при значении nINTk равна sINTk. В нашем случае каждый индекс нормирован и принимает значения в интервале [0; 1]. Таким образом, эластичность ВРП российских регионов по интегральному индексу структурной сложности принимает значения в интервале [0; s]. При изменении значения интегрального индекса на x%, изменение ВРП региона, не специализирующегося на добыче нефти и природного газа, оценивается в sINTkx%. Надо подчеркнуть, что оцениваемый здесь рост ВРП является относительным, то есть дополнительным к росту ВРП вследствие воздействия прочих факторов (время, научно-технический прогресс и др.). У региона, специализирующегося на добыче нефти и газа, рост структурной сложности экономики может быть вызван появлением новых сильных ВЭД, обусловленным развитием добывающего сектора. В этом случае доля природной ренты в ВРП может сохраняться и эластичность ВРП по интегральному индексу структурной сложности будет такой же, как у региона, не занимающегося добычей. Однако, для восьми регионов, специализирующихся на добыче нефти и природного газа, повышение структурной сложности экономики не обязательно сопровождается ростом объема добычи, приносящей природную ренту. Он может быть следствием появления в регионе новых сильных ВЭД, не связанных с добычей и не приносящих природной ренты. В этом случае оценка эластичности ВРП по интегральному индексу будет exp(-rk)snINTk, где
![]()
– оценка природной ренты, (-rk) – доля ВРП региона без учета природной ренты, а 1- exp(-rk) — доля природной ренты в ВРП. Поэтому для региона, получающего природную ренту от добычи нефти и природного газа, величину snINTk следует рассматривать как оценку сверху эластичности ВРП по структурной сложности. А величину exp(-rk)snINTk – как оценку снизу. Однако, оценка природной ренты в виде учитывает влияние на ВРП множества факторов, не отражающих специализацию региональных экономик. В то время как основным объединяющим эти регионы обстоятельством в нашем случае является их специализация на добыче нефти и природного газа. В данном исследовании мы не рассматриваем задачу оценки природной ренты каждого региона. В нашу задачу входит установить, как учет природной ренты, отражающий общую специализацию группы регионов, влияет на эластичность ВРП по значению интегрального индекса. А также обосновать на этой основе выбор значения параметра для целей прогнозирования и априорного оценивания влияния сложности структур занятости на ВРП. Поэтому далее мы рассмотрим альтернативный подход к оценке влияния сложности структур занятости на ВРП, который учитывает наличие природной ренты, являющейся общим результатом специализации группы регионов.
Рассмотрим модификацию производственной функции (4):
![]() (5)
(5)
в которой dk – булева переменная, принимающая значения 1 для группы регионов с общей специализацией, по совокупности которых оценивается природная рента. r – оценка природной ренты. Аналогичный подход к оценке природной ренты добывающих регионов использован в (Айвазян и др., 2018). Оценив параметры этой функции, мы можем оценить эластичность ВРП по значению индекса nINT структурной сложности для всей совокупности рассматриваемых регионов. При этом доля ВРП каждого из восьми регионов без учета природной ренты составляет exp(-r), а доля природной ренты в ВРП составляет 1- exp(-r).
Оценка параметра INT4 при интегральном индексе значима на 5%-м уровне и равна 0,298 (см. столбец (7) табл. 4). При этом значении оценка 1- exp(-r) доли природной ренты для восьми регионов равна 0,2558 и не превосходит доли природной ренты добывающих регионов, оцененной в работах (Айвазян и др., 2018). Оцененная доля exp(-r) ВРП после исключения природной ренты оставляет 0,742.
Таблица 4. Оценки параметров функции (6) для 85 регионов
| (1) | (2) | (4) | (5) | (6) | (7) |
| nINT1 | nINT2 | nINT3 | nINT4 | ||
| α t-статистика p-значение |
0,217*** (4,92) 0,000 |
0,208*** (4,73) 0,000 |
0,210*** (4,76) 0,000 |
0,214*** (4,75) 0,000 |
0,210*** (4,82) 0,000 |
| β t-статистика p-значения |
0,770*** (19,34) 0,000 |
0,759*** (19,01) 0,000 |
0,759*** (18,94) 0,000 |
0,766*** (18,79) 0,000 |
0,753*** (18,78) 0,000 |
| s t-статистика p-значение |
0,252* (1,70) 0,094 |
0,226 (1,56) 0,124 |
0,105 (0,56) 0,577 |
0,298** (2,02) 0,047 |
|
| r t-статистика p-значение |
0,213*** (2,70) 0,008 |
0,279*** (3,21) 0,002 |
0,273*** (3,13) 0,002 |
0,242** (2,55) 0,013 |
0,284*** (3,32) 0,001 |
| const t-статистика p-значение |
5,790*** (19,53) 0,000 |
6,080*** (16,19) 0,000 |
5,985*** (18,74) 0,000 |
5,865*** (17,97) 0,000 |
6,057*** (18,83) 0,000 |
| N | 85 | 85 | 85 | 85 | 85 |
| 0,9688 | 0,9699 | 0,9697 | 0,9689 | 0,9702 |
***значимость оценки на 1%-м уровне
**значимость оценки на 5%-м уровне
*значимость оценки на 10%-м уровне
Индекс nINT4 показывает лучшие статистические характеристики при оценке производственной функции (5) по данным 2022 года. Потому мы будем рассматривать его как основной интегральный индекс структурной сложности региональных экономик. Оценку 0,298 мы будем использовать при оценке эластичности ВРП по интегральному индексу nINT4 структурной сложности региональной экономики. А именно, в качестве оценки эластичности влияния структурной сложности на ВРП региона, не специализирующегося на добыче нефти и природного газа, будем рассматривать величину 0,298 nINT4. Например, для Владимирской области при значении в 2022 году nINT4=0.245 относительное повышение интегральной оценки сложности на 10% до величины 0,27 приводит к оценке относительного роста ВРП приблизительно на 0,73%. А для Калининградской области при значении nINT4=0.537 относительное повышение интегральной оценки сложности на 10% до величины 0,59 приводит к относительному росту ВРП приблизительно на 1,6%. Для регионов, получающих природную ренту от добычи нефти и природного газа, будем использовать оценку эластичности сверху 0.298*nINT4 и оценку эластичности снизу 0.742*0.298*nINT4. Например, для Оренбургской области при значении nINT4=0.065 относительное повышение интегральной оценки сложности на 70% до величины 0,111 приводит к оценке относительного роста ВРП в интервале [1,0 %; 1,3 %].
Заключение
На основе четырех базовых индексов экономической сложности (индекс сложности структур ВРП по данным об объемах производства по ВЭД; индекс сложности структур занятости регионов по профгруппам; индекс сложности структур занятости регионов по ВЭД; индекс сложности структур распределения предприятий в регионах по ВЭД) построены четыре интегральные индексы структурной сложности региональных экономик. Предложен подход к оценке влияния структурной сложности региональных экономик на ВРП. Построены производственные функции, включающие интегральный индекс структурной сложности. Показано, что структурная сложность региональной экономики оказывает влияние на ВРП региона. Получены оценки эластичности ВРП по интегральному индексу структурной сложности. По данным 2022 года интегральный индекс nINT4 показывает лучшие статистические характеристики при оценке модифицированной производственной функции.
Интегральный индекс структурной сложности региональных экономик позволяет комплексно оценить экономический потенциал территорий, выявить наиболее перспективные отрасли и производства, а также обозначить направления диверсификации, которые способствуют укреплению экономической безопасности регионов в условиях санкционного давления. Это закладывает фундамент для разработки обоснованных стратегий пространственных развития, направленных на увеличение экономической сложности и устойчивости региональных экономик.
Литература
- Айвазян, С.А. (2012) Анализ качества и образа жизни населения (эконометрический подход) / Москва, Издательство «Наука». – 432 с. – ISBN 978-5-02-037968-8. – EDN WNTANH.
- Айвазян, С.А., Афанасьев, М.Ю., Кудров, А.В. (2016). Модели производственного потенциала и оценки технологической эффективности регионов РФ с учетом структуры производства // Экономика и математические методы, 52 (1), 28–44.
- Айвазян, С.А., Афанасьев, М.Ю., Кудров, А.В. (2018) Об учете природной ренты в индикаторах регионального развития //Вестник ЦЭМИ РАН , – T. 1, №1. DOI: 10.33276/S0000006-9-1
- Афанасьев, М.Ю., Гусев, А.А. (2023). Ситуационное моделирование траекторий экономической сложности регионов // Экономика и математические методы. Т. 59. № 4. С. 58–70. DOI: 10.31857/S042473880028217-7
- Афанасьев, М.Ю., Гусев, А.А., Нанавян, А.М. (2023) Оценка профессиональной структуры занятого населения в российских регионах на основе концепции экономической сложности / Экономические и социальные перемены: факты, тенденции, прогноз. – Т. 16, № 6. – С. 91-107. – DOI 10.15838/esc.2023.6.90.5. – EDN DAPQSE.
- Афанасьев, М.Ю., Ильин, Н.И. (2022) Новые ориентиры для выбора приоритетных направлений диверсификации экономики на базе системы ситуационных центров / Экономика и математические методы. 2022. Том 58, №4. С. 29-44. DOI: 10.31857/S042473880023017-7
- Афанасьев, М.Ю., Кудров, А.В. (2021) Экономическая сложность и вложенность структур региональных экономик // Экономика и математические методы, т 57, № 3, стр. 67-78, DOI: 10.31857/S042473880016410-0
- Гусев, А.А. (2025) Сравнительный анализ подходов к оценке экономической сложности регионов России по структуре ВРП// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. —№3 (79). Номер статьи: 7917. Дата публикации: 22.09.2024. Режим доступа: https://eee-region.ru/article/7917/
- Hartmann, D. (2017) Linking economic complexity, institutions, and income inequality. World Development, 93, 75–93.
- Hidalgo, C. A. (2021) Economic complexity theory and applications. Nature Reviews Physics; 3(2), 92–113
- Hidalgo, C.A., Hausmann, R. (2009) The building blocks of economic complexity. Proceedings of the National Academy of Sciences, 106 (26), 10570–10575.
References
- Aivazian, S.A. Analysis of the Quality and Lifestyle of the Population (Econometric Approach) [Analiz kachestva i obraza zhizni naseleniya (ekonometricheskii podkhod)]. // Nauka Publishing House, 2012. — 432 p. ISBN 978-5-02-037968-8. – EDN WNTANH.
- Aivazian, S.A., Afanasyev, M.Yu., Kudrov, A.V. Models of Production Potential and Assessment of Technological Efficiency of Russian Regions, Taking into Account the Structure of Production [Modeli proizvodstvennogo potentsiala i otsenki tekhnologicheskoi effektivnosti regionov RF s uchetom struktury proizvodstva]. // Economics and Mathematical Methods, 52 (1), 2016, 28–44.
- Aivazian, S.A., Afanasyev, M.Yu., Kudrov, A.V. On Accounting for Natural Rent in Indicators of Regional Development [Ob uchete prirodnoi renty v indikatorakh regional’nogo razvitiya]. // Bulletin of CEMI RAS, Vol. 1, No. 1, 2018. DOI: 10.33276/S0000006-9-1
- Afanasyev, M.Yu., Gusev, A.A. Situational Modeling of Economic Complexity Trajectories of Regions [Situatsionnoe modelirovanie traektorii ekonomicheskoi slozhnosti regionov]. // Economics and Mathematical Methods, Vol. 59, No. 4, 2023, pp. 58–70. DOI: 10.31857/S042473880028217-7
- Afanasyev, M.Yu., Gusev, A.A., Nanavyan, A.M. Assessment of the Professional Structure of the Employed Population in Russian Regions Based on the Concept of Economic Complexity [Otsenka professional’noi struktury zanyatogo naseleniya v rossiiskikh regionakh na osnove kontseptsii ekonomicheskoi slozhnosti]. // Economic and Social Changes: Facts, Trends, Forecast, Vol. 16, No. 6, 2023, pp. 91-107. DOI 10.15838/esc.2023.6.90.5. – EDN DAPQSE.
- Afanasyev, M.Yu., Ilyin, N.I. New Benchmarks for Selecting Priority Areas for Economic Diversification Based on a System of Situational Centers [Novye orientiry dlya vybora prioritetnykh napravlenii diversifikatsii ekonomiki na baze sistemy situatsionnykh tsentrov]. // Economics and Mathematical Methods, Vol. 58, No. 4, 2022, pp. 29-44. DOI: 10.31857/S042473880023017-7
- Afanasyev, M.Yu., Kudrov, A.V. Economic Complexity and Embeddedness of Structures of Regional Economies [Ekonomicheskaya slozhnost’ i vlozhennost’ struktur regional’nykh ekonomik]. // Economics and Mathematical Methods, Vol. 57, No. 3, 2021, pp. 67-78. DOI: 10.31857/S042473880016410-0
- Gusev, A.A. Comparative analysis of approaches to assessing the economic complexity of Russian regions by the structure of GRP// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №3 (79). Art. #7917. Date issued: 22.09.2024. Available at: https://eee-region.ru/article/7917/
- Hartmann, D. (2017) Linking economic complexity, institutions, and income inequality. World Development, 93, 75–93.
- Hidalgo, C. A. (2021) Economic complexity theory and applications. Nature Reviews Physics; 3(2), 92–113
- Hidalgo, C.A., Hausmann, R. (2009) The building blocks of economic complexity. Proceedings of the National Academy of Sciences, 106 (26), 10570–10575.
Приложение
Таблица П1. Базовые и интегральные индексы по данным 2022 г.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| Ранг
INT1 |
Регион | nINT1 | nINT2 | nINT3 | nINT4 | Ранг
INT2 |
Ранг
INT3 |
Ранг
INT4 |
||||
| 1 | г. Москва | 1,0000 | 0,9364 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1 | 1 | 1 |
| 2 | г. Санкт-Петербург | 0,8938 | 0,9364 | 0,8850 | 0,7946 | 0,8581 | 0,8662 | 0,8546 | 0,8754 | 2 | 2 | 2 |
| 3 | Новосибирская область | 0,9077 | 0,8605 | 0,7216 | 0,3897 | 0,6448 | 0,6685 | 0,7127 | 0,6137 | 3 | 3 | 3 |
| 4 | Московская область | 0,8038 | 0,8326 | 0,6678 | 0,4192 | 0,6004 | 0,6195 | 0,6385 | 0,5979 | 4 | 4 | 4 |
| 5 | Томская область | 0,6145 | 1,0000 | 0,5903 | 0,4568 | 0,5823 | 0,6001 | 0,5233 | 0,5579 | 5 | 9 | 6 |
| 6 | Тюменская область без ао | 0,6145 | 0,5872 | 0,6944 | 0,6050 | 0,5451 | 0,5498 | 0,5612 | 0,5752 | 6 | 7 | 5 |
| 7 | Калининградская область | 0,7290 | 0,4626 | 0,7255 | 0,5221 | 0,5224 | 0,5303 | 0,6107 | 0,5370 | 8 | 5 | 7 |
| 8 | г. Севастополь | 0,7041 | 0,8087 | 0,8105 | 0,1743 | 0,5053 | 0,5487 | 0,5769 | 0,4746 | 7 | 6 | 8 |
| 9 | Приморский край | 0,7339 | 0,5554 | 0,6327 | 0,3173 | 0,4494 | 0,4677 | 0,5438 | 0,4654 | 9 | 8 | 9 |
| 10 | Самарская область | 0,6209 | 0,3901 | 0,5913 | 0,5441 | 0,4400 | 0,4385 | 0,5011 | 0,4584 | 11 | 13 | 10 |
| 11 | Нижегородская область | 0,7620 | 0,5657 | 0,5297 | 0,2954 | 0,4265 | 0,4405 | 0,5199 | 0,4353 | 10 | 10 | 11 |
| 12 | Кабардино-Балкарская Респ. | 0,6743 | 0,7947 | 0,4686 | 0,0749 | 0,3656 | 0,3965 | 0,4177 | 0,3412 | 12 | 19 | 13 |
| 13 | Краснодарский край | 0,7944 | 0,5275 | 0,5665 | 0,1107 | 0,3653 | 0,3923 | 0,5088 | 0,3527 | 13 | 11 | 12 |
| 14 | Свердловская область | 0,7709 | 0,3901 | 0,2563 | 0,3856 | 0,3419 | 0,3307 | 0,4358 | 0,3228 | 17 | 17 | 16 |
| 15 | Ивановская область | 0,7885 | 0,4996 | 0,3710 | 0,1990 | 0,3383 | 0,3481 | 0,4539 | 0,3288 | 14 | 15 | 14 |
| 16 | Калужская область | 0,7465 | 0,3317 | 0,6997 | 0,0746 | 0,3135 | 0,3463 | 0,5057 | 0,2962 | 15 | 12 | 19 |
| 17 | Ростовская область | 0,6668 | 0,4930 | 0,3959 | 0,2193 | 0,3112 | 0,3220 | 0,3967 | 0,3261 | 18 | 21 | 15 |
| 18 | Республика Крым | 0,7418 | 0,4626 | 0,5197 | 0,0798 | 0,3056 | 0,3311 | 0,4508 | 0,3025 | 16 | 16 | 17 |
| 19 | Респ. Северная Осетия–Алания | 0,7418 | 0,5867 | 0,3038 | 0,1082 | 0,2968 | 0,3112 | 0,3905 | 0,2811 | 19 | 25 | 21 |
| 20 | Воронежская область | 0,7582 | 0,5426 | 0,2698 | 0,1489 | 0,2960 | 0,3046 | 0,3936 | 0,2792 | 20 | 23 | 22 |
| 21 | Челябинская область | 0,7304 | 0,1982 | 0,5199 | 0,2640 | 0,2948 | 0,3023 | 0,4644 | 0,2885 | 21 | 14 | 20 |
| 22 | Ярославская область | 0,7698 | 0,3580 | 0,3292 | 0,2000 | 0,2806 | 0,2850 | 0,4183 | 0,2717 | 24 | 18 | 25 |
| 23 | Республика Карелия | 0,6376 | 0,4154 | 0,4792 | 0,1646 | 0,2800 | 0,2975 | 0,3917 | 0,3002 | 22 | 24 | 18 |
| 24 | Республика Алтай | 0,6960 | 0,5275 | 0,3038 | 0,1409 | 0,2772 | 0,2885 | 0,3669 | 0,2759 | 23 | 31 | 24 |
| 25 | Республика Адыгея | 0,7874 | 0,5807 | 0,1378 | 0,1296 | 0,2751 | 0,2783 | 0,3627 | 0,2317 | 26 | 32 | 35 |
| 26 | Республика Бурятия | 0,6875 | 0,4052 | 0,1874 | 0,3051 | 0,2710 | 0,2625 | 0,3476 | 0,2621 | 29 | 39 | 27 |
| 27 | Омская область | 0,6707 | 0,4296 | 0,2513 | 0,2296 | 0,2606 | 0,2612 | 0,3459 | 0,2637 | 30 | 40 | 26 |
| 28 | Ленинградская область | 0,6017 | 0,3329 | 0,5853 | 0,1308 | 0,2589 | 0,2830 | 0,3948 | 0,2777 | 25 | 22 | 23 |
| 29 | Республика Калмыкия | 0,7630 | 0,5275 | 0,2809 | 0,0409 | 0,2550 | 0,2710 | 0,3758 | 0,2330 | 27 | 26 | 33 |
| 30 | Чеченская Республика | 0,6212 | 0,5762 | 0,2173 | 0,1525 | 0,2493 | 0,2568 | 0,2999 | 0,2477 | 33 | 51 | 29 |
| 31 | Карачаево-Черкесская Респ. | 0,7845 | 0,5107 | 0,2173 | 0,0574 | 0,2469 | 0,2577 | 0,3682 | 0,2165 | 32 | 30 | 40 |
| 32 | Республика Дагестан | 0,6895 | 0,5762 | 0,2173 | 0,0791 | 0,2435 | 0,2552 | 0,3232 | 0,2282 | 34 | 45 | 37 |
| 33 | Владимирская область | 0,6859 | 0,2760 | 0,5438 | 0,0876 | 0,2424 | 0,2650 | 0,4151 | 0,2455 | 28 | 20 | 30 |
| 34 | Волгоградская область | 0,6410 | 0,4238 | 0,4103 | 0,1029 | 0,2424 | 0,2602 | 0,3569 | 0,2576 | 31 | 35 | 28 |
| 35 | Ставропольский край | 0,6493 | 0,4236 | 0,4381 | 0,0338 | 0,2259 | 0,2498 | 0,3564 | 0,2358 | 35 | 36 | 32 |
| 36 | Респ. Башкортостан | 0,6343 | 0,3522 | 0,3985 | 0,1236 | 0,2241 | 0,2384 | 0,3480 | 0,2408 | 36 | 38 | 31 |
| 37 | Хабаровский край | 0,6578 | 0,2760 | 0,4651 | 0,0892 | 0,2136 | 0,2320 | 0,3718 | 0,2235 | 37 | 27 | 39 |
| 38 | Мурманская область | 0,6359 | 0,2650 | 0,3985 | 0,1557 | 0,2114 | 0,2217 | 0,3494 | 0,2257 | 40 | 37 | 38 |
| 39 | Астраханская область | 0,5456 | 0,4996 | 0,3594 | 0,0729 | 0,2091 | 0,2287 | 0,2835 | 0,2305 | 38 | 57 | 36 |
| 40 | Еврейская автономная обл. | 0,6693 | 0,4402 | 0,3490 | 0,0176 | 0,2081 | 0,2282 | 0,3344 | 0,2109 | 39 | 43 | 41 |
| 41 | Алтайский край | 0,8029 | 0,2170 | 0,1750 | 0,1920 | 0,2074 | 0,2003 | 0,3712 | 0,1721 | 45 | 28 | 49 |
| 42 | Псковская область | 0,6888 | 0,3728 | 0,2261 | 0,1158 | 0,2002 | 0,2055 | 0,3188 | 0,1974 | 44 | 47 | 42 |
| 43 | Республика Тыва | 0,6280 | 0,5807 | 0,1475 | 0,0580 | 0,1990 | 0,2088 | 0,2593 | 0,1846 | 43 | 65 | 45 |
| 44 | Сахалинская область | 0,4489 | 0,2708 | 0,5311 | 0,1838 | 0,1976 | 0,2152 | 0,2951 | 0,2318 | 41 | 53 | 34 |
| 45 | Смоленская область | 0,7399 | 0,1586 | 0,2530 | 0,2057 | 0,1953 | 0,1910 | 0,3611 | 0,1767 | 47 | 33 | 48 |
| 46 | Брянская область | 0,6972 | 0,2458 | 0,4237 | 0,0528 | 0,1930 | 0,2105 | 0,3698 | 0,1932 | 42 | 29 | 43 |
| 47 | Рязанская область | 0,7003 | 0,4147 | 0,0690 | 0,1564 | 0,1910 | 0,1857 | 0,2822 | 0,1666 | 49 | 58 | 52 |
| 48 | Саратовская область | 0,6589 | 0,4236 | 0,2252 | 0,0764 | 0,1902 | 0,1994 | 0,2966 | 0,1905 | 46 | 52 | 44 |
| 49 | Камчатский край | 0,7444 | 0,2708 | 0,1882 | 0,1403 | 0,1879 | 0,1867 | 0,3351 | 0,1699 | 48 | 42 | 51 |
| 50 | Ульяновская область | 0,7067 | 0,4268 | 0,0897 | 0,1162 | 0,1867 | 0,1854 | 0,2854 | 0,1636 | 50 | 56 | 53 |
| 51 | Республика Ингушетия | 0,6630 | 0,5107 | 0,0000 | 0,1217 | 0,1760 | 0,1716 | 0,2363 | 0,1423 | 54 | 70 | 60 |
| 52 | Тверская область | 0,7541 | 0,3552 | 0,1025 | 0,0876 | 0,1736 | 0,1728 | 0,3056 | 0,1444 | 53 | 50 | 57 |
| 53 | Республика Коми | 0,6331 | 0,1950 | 0,4100 | 0,0910 | 0,1685 | 0,1821 | 0,3327 | 0,1783 | 51 | 44 | 47 |
| 54 | Липецкая область | 0,6360 | 0,1950 | 0,2908 | 0,1605 | 0,1650 | 0,1674 | 0,3076 | 0,1715 | 57 | 48 | 50 |
| 55 | Новгородская область | 0,6550 | 0,3692 | 0,1306 | 0,1191 | 0,1649 | 0,1648 | 0,2664 | 0,1584 | 58 | 61 | 55 |
| 56 | Пензенская область | 0,7199 | 0,2792 | 0,2304 | 0,0637 | 0,1643 | 0,1709 | 0,3200 | 0,1544 | 56 | 46 | 56 |
| 57 | Магаданская область | 0,5260 | 0,4094 | 0,3012 | 0,0571 | 0,1555 | 0,1710 | 0,2418 | 0,1797 | 55 | 68 | 46 |
| 58 | Тульская область | 0,6360 | 0,2062 | 0,3250 | 0,0952 | 0,1523 | 0,1612 | 0,3064 | 0,1609 | 59 | 49 | 54 |
| 59 | Кировская область | 0,7381 | 0,3114 | 0,0404 | 0,1200 | 0,1519 | 0,1447 | 0,2784 | 0,1186 | 62 | 60 | 69 |
| 60 | Пермский край | 0,5043 | 0,0000 | 0,6753 | 0,1254 | 0,1516 | 0,1746 | 0,3448 | 0,1440 | 52 | 41 | 58 |
| 61 | Курганская область | 0,6772 | 0,4031 | 0,1383 | 0,0331 | 0,1513 | 0,1578 | 0,2658 | 0,1394 | 60 | 62 | 61 |
| 62 | Удмуртская Республика | 0,5705 | 0,2170 | 0,0739 | 0,3012 | 0,1477 | 0,1299 | 0,2261 | 0,1382 | 64 | 74 | 62 |
| 63 | Вологодская область | 0,6940 | 0,1586 | 0,1718 | 0,1447 | 0,1364 | 0,1319 | 0,2931 | 0,1225 | 63 | 54 | 66 |
| 64 | Архангельская область без ао | 0,6793 | 0,0000 | 0,4474 | 0,0893 | 0,1356 | 0,1466 | 0,3575 | 0,1187 | 61 | 34 | 68 |
| 65 | Чувашская Республика | 0,6645 | 0,1683 | 0,1963 | 0,1208 | 0,1270 | 0,1259 | 0,2804 | 0,1216 | 67 | 59 | 67 |
| 66 | Чукотский автономный округ | 0,5272 | 0,3062 | 0,2358 | 0,0899 | 0,1213 | 0,1288 | 0,2190 | 0,1438 | 65 | 75 | 59 |
| 67 | Орловская область | 0,6789 | 0,3661 | 0,0404 | 0,0429 | 0,1195 | 0,1191 | 0,2319 | 0,0975 | 68 | 72 | 73 |
| 68 | Кемеровская область | 0,5604 | 0,1066 | 0,2654 | 0,1793 | 0,1154 | 0,1139 | 0,2529 | 0,1255 | 70 | 67 | 65 |
| 69 | Забайкальский край | 0,5528 | 0,1964 | 0,3490 | 0,0542 | 0,1133 | 0,1267 | 0,2575 | 0,1339 | 66 | 66 | 64 |
| 70 | Республика Татарстан | 0,4007 | 0,1586 | 0,3269 | 0,1991 | 0,1024 | 0,1056 | 0,1910 | 0,1344 | 71 | 77 | 63 |
| 71 | Амурская область | 0,6005 | 0,1066 | 0,3933 | 0,0176 | 0,1001 | 0,1159 | 0,2859 | 0,1078 | 69 | 55 | 71 |
| 72 | Костромская область | 0,7247 | 0,1964 | 0,0690 | 0,0637 | 0,1001 | 0,0957 | 0,2601 | 0,0730 | 74 | 64 | 76 |
| 73 | Белгородская область | 0,4955 | 0,1586 | 0,1199 | 0,2505 | 0,0991 | 0,0866 | 0,1840 | 0,1062 | 75 | 78 | 72 |
| 74 | Республика Мордовия | 0,6583 | 0,1586 | 0,2189 | 0,0331 | 0,0947 | 0,1005 | 0,2652 | 0,0919 | 72 | 63 | 74 |
| 75 | Республика Хакасия | 0,5691 | 0,1964 | 0,2397 | 0,0632 | 0,0938 | 0,1004 | 0,2306 | 0,1085 | 73 | 73 | 70 |
| 76 | Республика Марий Эл | 0,6677 | 0,1586 | 0,1025 | 0,0714 | 0,0822 | 0,0789 | 0,2380 | 0,0689 | 77 | 69 | 77 |
| 77 | Иркутская область | 0,5554 | 0,1066 | 0,2930 | 0,0571 | 0,0746 | 0,0827 | 0,2334 | 0,0889 | 76 | 71 | 75 |
| 78 | Тамбовская область | 0,6951 | 0,2506 | 0,0244 | 0,0000 | 0,0706 | 0,0695 | 0,2178 | 0,0457 | 78 | 76 | 82 |
| 79 | Оренбургская область | 0,4598 | 0,3355 | 0,0552 | 0,0607 | 0,0504 | 0,0510 | 0,1130 | 0,0645 | 79 | 82 | 78 |
| 80 | Республика Саха (Якутия) | 0,4035 | 0,0000 | 0,3542 | 0,1352 | 0,0399 | 0,0453 | 0,1767 | 0,0621 | 80 | 79 | 79 |
| 81 | Ханты-Мансийский ао | 0,1654 | 0,0000 | 0,5319 | 0,1839 | 0,0274 | 0,0416 | 0,1129 | 0,0504 | 81 | 83 | 81 |
| 82 | Красноярский край | 0,3914 | 0,1586 | 0,2476 | 0,0594 | 0,0260 | 0,0340 | 0,1278 | 0,0605 | 82 | 81 | 80 |
| 83 | Ямало-Ненецкий ао | 0,1654 | 0,0000 | 0,5319 | 0,1361 | 0,0093 | 0,0266 | 0,1026 | 0,0352 | 83 | 84 | 83 |
| 84 | Курская область | 0,5772 | 0,1066 | 0,0647 | 0,0000 | 0,0010 | 0,0000 | 0,1537 | 0,0000 | 85 | 80 | 85 |
| 85 | Ненецкий ао | 0,0000 | 0,1048 | 0,4180 | 0,2494 | 0,0000 | 0,0074 | 0,0000 | 0,0274 | 84 | 85 | 84 |