Разработка и анализ модели взаимовлияния социальной, экономической и военной систем для государственного и регионального управления
Development and analysis of the model of mutual influence of social, economic and military systems for state and regional management
Авторы
Аннотация
В работе приведена модель взаимовлияния социальной, экономической и военной систем, разработанная для поддержки принятия решения при управлении государством или регионом. Недостатком модели является неочевидность трактовки результатов моделирования, поэтому в работе приведено обоснование физического смысла получаемых результатов и принципы их трактовки посредством использования фазовых портретов.
Ключевые слова
государственное и региональное управление, модель взаимовлияния социальной, экономической и военной систем, социальная система, экономическая система
Рекомендуемая ссылка
Разработка и анализ модели взаимовлияния социальной, экономической и военной систем для государственного и регионального управления// Региональная экономика и управление: электронный научный журнал. ISSN 1999-2645. — №2 (50). Номер статьи: 5020. Дата публикации: 26.05.2017. Режим доступа: https://eee-region.ru/article/5020/
Authors
Abstract
The paper presents a model of mutual influence of social, economic and military systems, designed to support decision-making in the management of the state or the region. The disadvantage of the model is the non-obvious interpretation of the results of modeling, therefore, the work substantiates the physical meaning of the results obtained and the principles of their interpretation through the use of phase portraits.
Keywords
State and regional management, the model of mutual influence of social, economic and military systems, the social system, the economic system
Suggested Citation
Development and analysis of the model of mutual influence of social, economic and military systems for state and regional management// Regional economy and management: electronic scientific journal. ISSN 1999-2645. — №2 (50). Art. #5020. Date issued: 26.05.2017. Available at: https://eee-region.ru/article/5020/
Введение
В соответствии с действующей «Стратегией национальной безопасности» утвержденной указом Президента №683 от 31 декабря 2015 первым приоритетом для реализации национальных интересов является «оборона страны», а уже потом социальные и экономические потребности (п.31 Стратегии) [1]. Учитывая настоящие непростые экономические и геополитические условия, для лица, принимающего решение в рамках государства или региона необходимым является соизмерение возможностей социальной и экономической систем, потребностям военной системы. В противном случае может произойти снижение потенциала военной системы при недостаточном ее финансировании или ослабление социальных и экономических возможностей государства в целом или рассматриваемого региона в частности. При этом: под социальной системой понимается – целостное образование, состоящее из взаимосвязанных компонентов в виде объектов, которыми могут быть как отдельные люди, так и группы людей страны, региона; под экономической системой понимается – целостное образование, состоящее из взаимосвязанных компонентов в виде продуктов деятельности юридических и физических лиц, занимающих производством и реализацией товаров и услуг страны, региона; под военной системой понимается – целостное образование, состоящее из взаимосвязанных (взаимозависимых) компонентов которыми могут быть военнослужащие, воинские части, военная техника [2].
Соответственно, можно утверждать, что развитие военной системы, как основы обеспечения обороны страны имеет высший приоритет. Вместе с тем есть социальные и экономические возможности и потребности, игнорирование которых в последствии неизбежно скажется на обороноспособности. Следовательно, необходимым является обеспечение соответствия объемов ассигнований, выделяемых на развитие военной системы социальным и экономическим возможностям страны и регионов.
Необходимо отметить, что приведенная задача в той или иной мере рассматривалась в работах следующих зарубежных и отечественных авторов: Benoit E, Alexander R., Biswas B., Blasko, D., Freeman C., Horowitz S., Medeiros E., Mulvenon J., Braddon D., Kollias C., Gold D., Deger S., Чернавский Д.С., Малков С.Ю., Старков Н.И., Коссее Ю.В., Хрусталев Е.Ю., Цымбал В.И., Садовничий В. А., Акаев А. А., Коротаев А. В., Малков С. Ю. [3-23]
Однако в работах приведенных авторов использовались модели, построенные на основе анализа, что не дает возможности формировать выходные параметры как заданные т.е. их использование не в полной мере обеспечивает гарантированное достижение поставленной цели, при управлении государством или регионом.
Модель взаимовлияния социальной, экономической и военной систем
В рамках данной работы построена модель взаимовлияния социальной, экономической и военной систем, посредством использования методологии В. Бурлова [2], где формализован критерий построения модели на основе синтеза, использование которого позволило построить модель в виде системы нелинейных дифференциальных уравнений, с возможностью задания входных данных как требуемых или заданных:
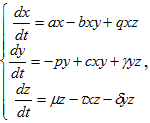, (1)
где:
x – переменная, являющаяся нормированной численностью населения в стране, регионе;
y – переменная, являющаяся нормированным ВВП на душу населения в стране, регионе;
z – переменная, являющаяся нормированными затраты на ВС на душу населения, в стране, регионе;
a – коэффициент, отражающий естественные демографические процессы в стране, регионе;
b – коэффициент антимотивации людей к деторождению, «1-2 ребёнка – допустимо, а 3-5 – уже надо подумать» в стране, регионе;
q – коэффициент защищенности населения, при отсутствии вооруженных конфликтов люди планируют семьи и будущее в стране, регионе;
p – коэффициент развития экономики, отражающий экономическое развитие в стране, регионе;
c – коэффициент заинтересованности людей в развитии экономики, для благополучия человеку необходимо трудиться, что положительно влияет на развитие экономики в стране, регионе;
γ – коэффициент защищенности экономики, при отсутствии вооруженных конфликтов в стране, регионе;
μ – коэффициент наращивания военных расходов, отражающий тенденции военных расходов в стране, регионе;
τ – коэффициент демографических возможностей страны по формированию военной системы в стране, регионе;
δ – коэффициент, экономических возможностей страны по содержанию и развитию военной системы в стране, регионе.
Для количественного задания приведенных параметров были выделены базовые составляющие социальной, экономической и военной подсистем и факторы, которые влияют на скорость изменения этих составляющих. Посредством разложения в ряд Тейлора и проведения линейно-кусочной аппроксимации выделенных функциональных зависимостей была разработана параметризация зависимостей системы дифференциальных уравнений взаимовлияния социальной, экономической и военной систем, позволившая рассчитать их используя общедоступные данные [24].
Достоверность адекватности построенной модели подтверждается сходимостью результатов моделирования на основании данных [24] за 2001-2009 гг. и полученного прогноза 2009-2015 гг. с реальной статистикой, что подтверждено в работе [25].
В тоже время, недостатком модели является неочевидность трактовки результатов моделирования для лица, принимающего решение. В этой вязи в данной работе приведен анализ и обоснование физического смысла получаемых результатов и принципы их трактовки необходимые для возможности поддержки принятия решения.
Решение системы уравнений модели взаимовлияния социальной, экономической и военной систем
Необходимо отметить отсутствие аналитического решения подобного радо систем уравнений, что было доказано в работе [26], соответственно решение возможно только посредством использования численных методов, которые заменяют непрерывную задачу дискретной. Задача Коши для такого рода уравнений детально изложена в теории колебаний, когда требуется найти непрерывные при 
траектории переменных 
, 
, 
, при 
и начальном условии 
.
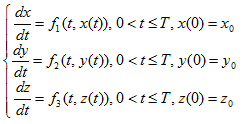(2)
при
, (3)
, (4)
, (5)
где заданные функции не явно зависимы от времени 
.
Для задачи такого типа целесообразно использовать метод Рунге-Кутты.
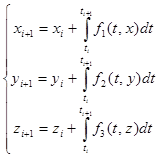(6)
Суть данного метода состоит в замене функций 
, 
, 
, некоторым приближением, чем точнее будет приближенное значение подынтегральной функции, тем точнее в итоге будет посчитан интеграл, т.е. тем точнее будут определены 
.
Таким образом, очевидно, что решение рассматриваемой системы уравнений наиболее целесообразно посредством применения метода Рунге-Кутты, который достаточно прост и дает приемлемые по точности результаты.
Оценка поведения траекторий в фазовом пространстве
Приведение рассматриваемой системы уравнений к матричному виду показал, что она является квадратичной:
(8)
где:
первая часть имеет линейную природу:
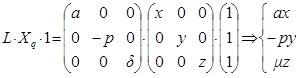(9)
вторая имеет квадратичную природу:
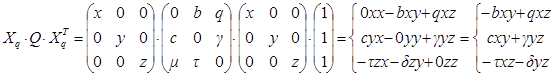(10)
Наличие квадратичной составляющей обуславливает целесообразность анализа решения опираясь на классическую теорию колебаний. Соответственно для анализа системы уравнений, целесообразно использовать фазовые портреты, которые достаточно полно и емко отражают свойства рассматриваемой функции [27]. При этом под фазовым портретом понимается совокупность всех ее траекторий, изображенных в пространстве фазовых переменных.
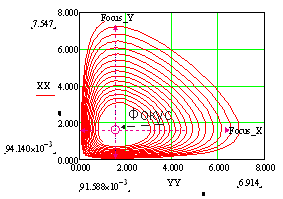
Учитывая, что рассматривается состояние из трех системообразующих показателей, наиболее полным является рассмотрение фазовых портретов в трехмерном пространстве, для более детального анализа целесообразно сопоставлять фазовые портреты трехмерного и двухмерного пространств. Пример такого анализа, при условно произвольных входных параметрах приведен на рисунке 1, где фазовый портрет в двухмерном пространстве представлен на рисунке 1 а и его фазовый портрет в трехмерном пространстве на рисунке 1 б.
 |
 |
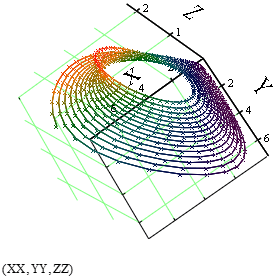| а) | б) |
Рисунок 1. Иллюстрация фазовых портретов системы
Соответственно, для возможности анализа результатов применения численного метода решения предложено использовать фазовые портреты, которые достаточно полно и емко отражают свойства рассматриваемой системы.
Для более обоснованной оценки и анализа локальных бифуркаций фазовых портретов вблизи особых точек и предельных циклов необходимо рассматривать только те значения входных параметров, когда система дифференциальных уравнений из состояния устойчивого равновесия вырождается или переходит в хаос.
Стоит отметить, что рассматриваемая система дифференциальных уравнений имеет точки устойчивости, где производные равны нулю: 
.
Такие точки, носят название особых точек данного дифференциального уравнения [27]. Рассматриваемая система уравнений может иметь много особых точек. Соответственно необходимо рассмотреть их все.
Квадратичная структура позволяет показать, что существует только 5 точек устойчивости
Принимая возможность, когда уместно рассмотреть следующую алгебраическую систему уравнений:
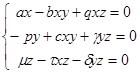(11)
преобразовав систему уравнения к следующему виду:
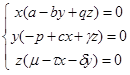(12)
не трудно удостовериться, что особыми, будут является следующие точки:
Особая точка №1:
(13)
Очевидно, что существование данной точки лишено физического смысла для рассматриваемой системы. Так, как все системообразующие показатели равны нулю, – отсутствуют. Система вырождена.
Особая точка №2:
, (y, z – решения уравнений);
(14)
Очевидно, что существование данной точки лишено физического смысла для рассматриваемой системы. Так, как социальная система отсутствует. Система не может существовать когда .
Особая точка №3:
(x, z – решения уравнений);
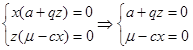(15)
Очевидно, что существование данной точки лишено физического смысла для рассматриваемой системы. Так как экономика отсутствует. Система не может существовать когда .
Особая точка №4:
(x, y – решения уравнений);
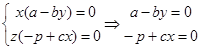(16)
Существование данной точки возможно. Теоретически государство может существовать без военной системы. Система может существовать когда . Данный случай не рассматривается.
Особая точка №5:
(x, y, z – решения уравнений);
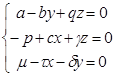(17)
Возможно существование только данной особой точки (Особая точка №5), физический смысл которой характеризует государство, как находящее в состоянии равновесия. Данную особую точку примем как фокус системы уравнений. Соответственно система уравнений для нахождения фокусов примет следующий вид:
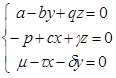(18)
Как было отмечено ранее, равенство нулю хотя бы одного из системообразующих показателей не имеет физического смысла, соответственно решения (13-15) будем считать вырожденными. Уравнение (16) имеет смысл, когда нет военных расходов, или влияние их на экономику незначительно (при этом 
, 
), данный случай не рассматривается. Поэтому практическую значимость имеет только невырожденная система уравнений (17).
Как было отмечено ране существование системы возможно только при условии, когда системообразующие показатели не равны нулю 
. При этом необходимо учесть, что устойчивой система будет тогда, когда приращение по каждому показателю будет равно нулю 
, что к тому же снижает амплитуду колебаний системообразующих показателей при допустимых входных параметрах.
Соответственно состояние равновесия в рамках рассматриваемой системы выполняется, при следующих условиях:
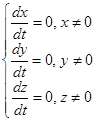(19)
Соответственно, для нахождения линий бифуркации необходимо рассмотреть следующую математическую интерпретацию рассматриваемой системы уравнений:
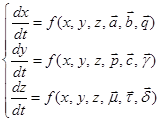(20)
где 
входные параметры рассматриваемой системы ОДУ.
Соответственно необходимо выяснить, как будет вести себя фазовый портрет данной системы при изменении вышеприведенных входных параметров, когда приращение отсутствует.
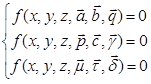(21)
Для иллюстрации в таблице 1 приведены типы устойчивости и сопутствующие им направления траекторий, а также шаблонные виды фазовых портретов.
Таблица 1. Тип устойчивости и вид фазового портрета
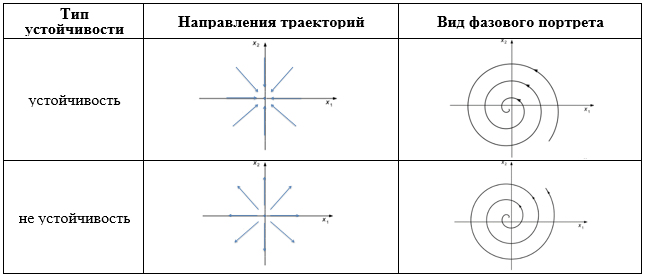
Для примера рассмотрим два варианта входных параметров, в которых незначительно отличается входной показатель μ. В обоих варианта рассматривается динамика от 10 (а) до 20(б) полных колебаний.
1 – вариант, характеризует систему как не устойчивую, т.е. колебания с течением времени расширяются до состояния вырождения системы (рисунок 2).
Значения входных показателей приняты произвольно равными: 
, 
, 
, 
, 
, 
, 
, 
, 
.
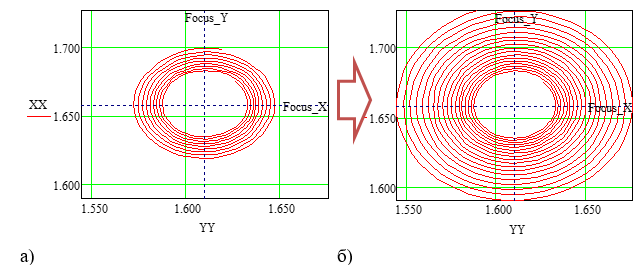
Рисунок 2. Фазовый портрет (10 и 20 колебаний)
2 – вариант, характеризует систему как устойчивую, т.е. колебания с течением времени приближаются к точке фокуса (рисунок 3)
Значения входных показателей приняты равными: , , , , , , 
, , .
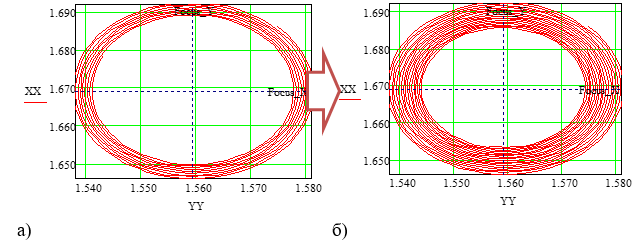
Рисунок 3. Фазовый портрет (10 и 20 колебаний)
В данном примере, на рассматриваемой системе иллюстрируется точка бифуркации. Когда незначительное уменьшение одного показателя μ с значения 1,59 до 1,58 система из неустойчивой преобразуется в устойчивую. Что может быть важным при принятии того или иного управленческого решения.
Заключение
Таким образом, в рамках данного исследования проведен анализ отечественного и зарубежного опыта оценки влияния расходов военной системы на развитие социальной и экономической систем, выявлено преимущественное использование моделей, построенных на основе анализа, что не дает возможности формировать выходные параметры как заданные т.е. их использование не в полной мере обеспечивает гарантированное достижение поставленной цели при управлении страной или регионом. Предложено использовать модель взаимовлияния социальной, экономической и военной систем, построенную на основе синтеза. Проведен анализа разработанной модели, позволивший обосновать целесообразность применения фазовых портретов для оценки результатов моделирования, что может использоваться для оценки влияния того или иного управленческого решения как на государственном уровне, так и на региональном.
Список использованных источников
- Указ Президента Российской Федерации от 31.12.2015 г. № 683 «О Стратегии национальной безопасности Российской Федерации». URL:http://kremlin.ru /dacts/bank/40391_Официальный сайт «Президента России» (http://www. kremlin.ru). (дата обращения 1.02.2017).
- Бурлов В.Г. Основы моделирования социально-экономических и политических процессов. Часть (Модели. Технологии.). С-Пб. НП «Стратегия будущего», 2007. -278 с.
- Benoit, Emile (1973), Defense and Economic Growth in Developing Countries (Lexington, MA: Lexington Books)
- Biswas, B. and R. Ram, 1986. Military expenditures and economic growth in less developed countries: An augmented model and further evidence. Economic Development and Cultural Change, 34(2): 361-372.
- Blasko, D.J., C.W. Freeman, S.A. Horowitz, E.S. Medeiros and J.C. Mulvenon,2007. Defense-related spending in China: A preliminary analysis and comparison with American equivalents: United States-China Policy Foundation. Chletsos, M. and C. Kollias, 1995. Defence spending and growth in Greece 1974–90: Some preliminary econometric results. Applied Economics, 27(9): 883-890.
- Braddon, Derek, 1995. ‘The Regional Impact of Defense Expenditure’, in Hartley & Sandler, 491–521.
- Christos Kollias & Charis Naxakisbb & Leonidas Zarangasbb Defence Spending and Growth in Cyprus: A Causal Analysis. Defense and Peace Economics 15.3: 299-307.
- Christos Kollias. Defence spending and growth in turkey 1954–1993: A causal analysis. Defense and Peace Economics 8.2: 189-204.
- Christos Kolliasa & Stelios Makrydakisb. A note on the causal relationship between defence spending and growth in Greece: 1955–93. Defence and the Israeli economy. Defense and Peace Economics 11.1: 173-184.
- David Gold. Evaluating the tradeoff between military spending and investment in the United States. Defense and Peace Economics 8.3: 251-266. (нет)
- Deger, S. and R. Smith, 1983. Military expenditure and growth in less developed countries. Journal of Conflict Resolution, 27(2): 335-353.
- Deger, S. and S. Sen, 1995. Military expenditure and developing countries. Handbook of Defense Economics, 1: 275-307.
- Deger, S., 1986. Economic development and defense expenditure. Economic Development and Cultural Change, 35(1): 179-196.
- Deger, Saadet & Somnath Sen, 1995. ‘Military Expenditure and Developing Countries’, in Hartley & Sandler 275–307.
- Deger, Saadet, 1986. ‘Economic Development and Defense Expenditure’, Economic Development and Cultural Change 35(1): 179–196.
- Чернавский Д.С., Малков С.Ю., Старков Н.И., Коссее Ю.В. Оборонно-промышленный комплекс и развитие экономики России // Стратегическая стабильность 2004. №1. с.37-47.
- Хрусталев Е.Ю., Цымбал В.И. Экономические проблемы обеспечения военной безопасности России / Центр. экон.-мат. ин-т, Рос. акад. наук. — М.: ЦЭМИ РАН, 2000. — 128 с.
- Садовничий В. А., Акаев А. А., Коротаев А. В., Малков С. Ю. Комплексное моделирование и прогнозирование развития сран БРИКС в контексте мировой динамики. — М.: Наука, 2014. — 382 С.
- Садовничий В.А., Акаев А.А., Коротаев А.В., Малков С.Ю. / Научный совет по Программе фундаментальных исследований Президиума Российской академии наук «Экономика и социология знания». — М.: ИСПИ РАН, 2012. — 359 с.
- Малков С.Ю. Социальная самоорганизация и исторический процесс: возможноси математического моделирования. М.:Либроком/URSS. 2009 — 236 с.
- Малков С.Ю., Чернавский Д.С., Ковалев В.И., Коссее Ю.В. Старков Н.И. Экономика России и обеспечение военно-стратегической стабильности // Стратегическая стабильность 2005. №1. с.67-74.
- Малков С.Ю., Чернавский Д.С., Коссе Ю.В., Влияние военных расходов на макроэкономические показатели // Стратегическая стабильность, №2 — 2008 г с 27-39.
- Малков С.Ю., Чернавский Д.С., Коссе Ю.В., К вопросу об определении оптимальной величины оборонных расходов государства // Стратегическая стабильность, №2 — 2007 г с 72-76, 2007.
- Официальный сайт Федеральной службы государственной статистики. URL:http://www.gks.ru. (дата обращения 1.02.2017).
- Пестун У.А., Патент на полезную модель «Устройство для оценки взаимовлияния социальной, экономической и военной систем государства», №168601, дата регистрации 10.02.2017 г., срок действия на полезную модель истекает 21.09.2026.
- J. Lotka (1925). Elements of Physical Biology, Williams and Wilkins, Baltimore (reprinted as Elements of Mathematical Biology, Dover, New York, 1956).
- Андронов А.А., Вит А.А., Хайкин С.Э. Теория колебаний. 2-е изд., перераб. и испр. – М.: Наука, 1981. — 918 с.
Bibliography
- Decree of the President of the Russian Federation of December 31, 2015, No. 683 «On the National Security Strategy of the Russian Federation [O Strategii nacional’noj bezopasnosti Rossijskoj Federacii]». URL: http: //www.kremlin.ru / dacts / bank / 40391_Official site of the «President of Russia» (http: // www. Kremlin.ru). (The date of circulation is 1.02.2017).
- Burlov V.G. Fundamentals of modeling of socio-economic and political processes. Part 1. (Models, Technologies.) [Osnovy modelirovanija social’no-jekonomicheskih i politicheskih processov. Chast’ 1. (Modeli. Tehnologii.)]. St.P. NP «Strategy of the Future», 2007. -278 p.
- Benoit, Emile (1973), Defense and Economic Growth in Developing Countries (Lexington, MA: Lexington Books)
- Biswas, B. and R. Ram, 1986. Military expenditures and economic growth in less developed countries: An augmented model and further evidence. Economic Development and Cultural Change, 34(2): 361-372.
- Blasko, D.J., C.W. Freeman, S.A. Horowitz, E.S. Medeiros and J.C. Mulvenon,2007. Defense-related spending in China: A preliminary analysis and comparison with American equivalents: United States-China Policy Foundation. Chletsos, M. and C. Kollias, 1995. Defence spending and growth in Greece 1974–90: Some preliminary econometric results. Applied Economics, 27(9): 883-890.
- Braddon, Derek, 1995. ‘The Regional Impact of Defense Expenditure’, in Hartley & Sandler, 491–521.
- Christos Kollias & Charis Naxakisbb & Leonidas Zarangasbb Defence Spending and Growth in Cyprus: A Causal Analysis. Defense and Peace Economics 15.3: 299-307.
- Christos Kollias. Defence spending and growth in turkey 1954–1993: A causal analysis. Defense and Peace Economics 8.2: 189-204.
- Christos Kolliasa & Stelios Makrydakisb. A note on the causal relationship between defence spending and growth in Greece: 1955–93. Defence and the Israeli economy. Defense and Peace Economics 11.1: 173-184.
- David Gold. Evaluating the tradeoff between military spending and investment in the United States. Defense and Peace Economics 8.3: 251-266. (нет)
- Deger, S. and R. Smith, 1983. Military expenditure and growth in less developed countries. Journal of Conflict Resolution, 27(2): 335-353.
- Deger, S. and S. Sen, 1995. Military expenditure and developing countries. Handbook of Defense Economics, 1: 275-307.
- Deger, S., 1986. Economic development and defense expenditure. Economic Development and Cultural Change, 35(1): 179-196.
- Deger, Saadet & Somnath Sen, 1995. ‘Military Expenditure and Developing Countries’, in Hartley & Sandler 275–307.
- Deger, Saadet, 1986. ‘Economic Development and Defense Expenditure’, Economic Development and Cultural Change 35(1): 179–196.
- Chernavskij D.S., Malkov S.Ju., Starkov N.I., Kossee Ju.V. The Defense Industry Complex and the Development of the Russian Economy [Oboronno-promyshlennyj kompleks i razvitie jekonomiki Rossii]// Strategic Stability 2004. No. 1. P.37-47.
- Hrustalev E.Ju., Cymbal V.I. Economic Problems of Ensuring Russia’s Military Security [Jekonomicheskie problemy obespechenija voennoj bezopasnosti Rossii]/ Center. Econ.-math. In-t, Ros. Acad. Sciences. — Moscow: CEMI RAS, 2000. — 128 p.
- Sadovnichij V. A., Akaev A. A., Korotaev A. V., Malkov S. Ju. Complex modeling and forecasting of BRICS development in the context of world dynamics [Kompleksnoe modelirovanie i prognozirovanie razvitija sran BRIKS v kontekste mirovoj dinamiki]. — Moscow: Nauka, 2014. — 382 С.
- Sadovnichij V.A., Akaev A.A., Korotaev A.V., Malkov S.Ju. Scientific Council on the Program of Fundamental Research of the Presidium of the Russian Academy of Sciences «Economics and Sociology of Knowledge» [Nauchnyj sovet po Programme fundamental’nyh issledovanij Prezidiuma Rossijskoj akademii nauk «Jekonomika i sociologija znanija»]. — Moscow: ISPI RAS, 2012. — 359 p.
- Malkov S.Ju. Social self-organization and historical process: the possibility of mathematical modeling [Social’naja samoorganizacija i istoricheskij process: vozmozhnosi matematicheskogo modelirovanija]. M.: Librocom / URSS. 2009 — 236 pp.
- Malkov S.Ju., Chernavskij D.S., Kovalev V.I., Kossee Ju.V. Starkov N.I. Economics of Russia and ensuring military-strategic stability [Jekonomika Rossii i obespechenie voenno-strategicheskoj stabil’nosti]// Strategic stability 2005. №1. P.67-74.
- Malkov S.Ju., Chernavskij D.S., Kosse Ju.V., Influence of military expenditures on macroeconomic indicators [Vlijanie voennyh rashodov na makrojekonomicheskie pokazateli] // Strategic Stability, №2 — 2008 from 27-39.
- Malkov S.Ju., Chernavskij D.S., Kosse Ju.V., On the question of determining the optimal value of defense expenditures of the state [K voprosu ob opredelenii optimal’noj velichiny oboronnyh rashodov gosudarstva] // Strategic Stability, №2 — 2007, from 72-76, 2007.
- Official website of the Federal State Statistics Service. (The date of circulation is 1.02.2017).
- Pestun U.A., patent for the utility model «Device for assessing the mutual influence of the social, economic and military systems of the state» [Patent na poleznuju model’ «Ustrojstvo dlja ocenki vzaimovlijanija social’noj, jekonomicheskoj i voennoj sistem gosudarstva»], No. 168601, registration date 10.02.2017, the validity period for the utility model expires on 21.09.2026.
- J. Lotka (1925). Elements of Physical Biology, Williams and Wilkins, Baltimore (reprinted as Elements of Mathematical Biology, Dover, New York, 1956).
- Andronov A.A., Vit A.A., Hajkin S.Je. The theory of oscillations [Teorija kolebanij]. 2 nd ed., Revised. And corrected. — Moscow: Nauka, 1981. — 918 p.
Еще в рубриках
Государственное и муниципальное управление